A Primer by AZTEC
How do you benchmark SNARKs?
It’s a problem because different SNARKs will perform differently on various circuits — it’s not a matter of ‘PLONK is 5x faster than Sonic every time’.
Well, a critical measure is how efficiently a SNARK can verify a hash operation. But why are hashes important? This article describes how zero-knowledge assets are stored in the Two-Tree Model, and therefore why fast hashes in SNARKs are mission-critical.
Merkle Trees: Refresher
Before explaining how the Two-Tree Model works, here’s a reminder of what a Merkle tree actually is.
Remember, the purpose of a Merkle Tree is to generate a single short digest (hash) of many pieces of data, so that if asked, one can prove that any one piece of data is ‘guaranteed’ by that hash without revealing all the other pieces of data.
In the diagram below, data pieces A, B, C and D are separately hashed. Next, each pair is hashed together (turning 4 hashes into two hashes). Finally, those two hashes are hashed to form the ‘Merkle Root’.
The Merkle Root changes if and only if a single piece of data changes (i.e. if A, B, C or D are modified / edited). Here’s the picture to have in mind:

SNARK Storage: The Two-Tree Model
We introduce the classical model for storing ZK Assets.
This system is built around a UTXO model like Bitcoin — i.e. each asset is recorded via so-called ‘notes’ of ownership. An asset with $1,000 total global supply is held in the form of one-or-more notes by each owner.
Alice may hold $10 of this asset in (say) three notes: $7, $2 and $1. Transferring ownership involves a ‘join split’ transaction which takes input notes (e.g. say the $7 and $2 notes above), and printing new output notes (say $8 and $1).
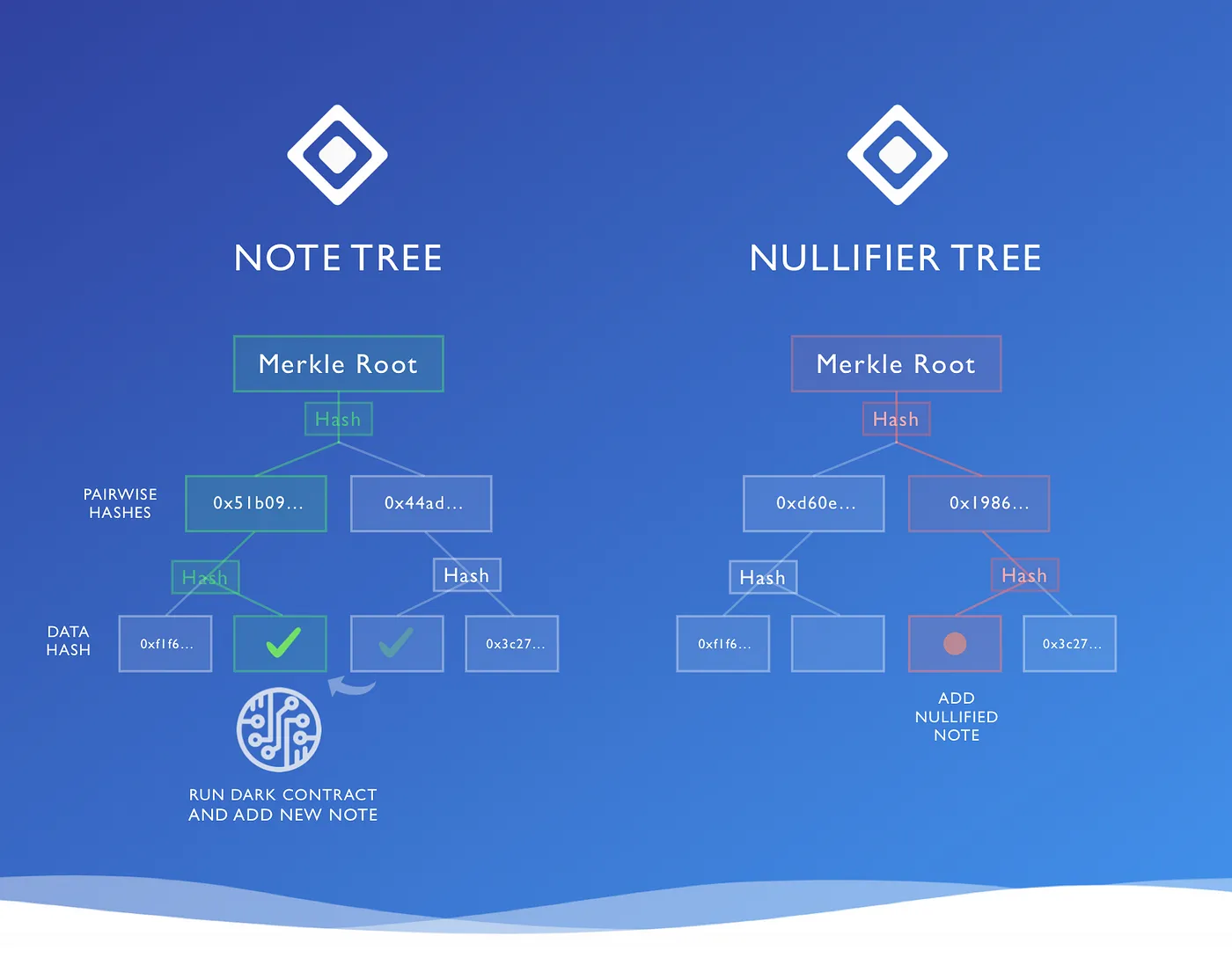
Instead of creating output notes and destroying input notes, we instead record this process in two trees —
- A Note Tree of all output notes ever created, and
- A Nullifier Tree keeping copies of the spent notes
The idea is — instead of deleting a note from the Note Tree, you need to check whether that note also turns up in the Nullifier Tree to work out if it’s already spent. If it’s not there, it’s still spendable.
A join-split transaction adds the output notes to the Note Tree, and the input notes to the Nullifier Tree.
Let’s take a closer look at these structures.
The Note Tree
Locations in Tree = ~2³⁰ leaves (dense Merkle Tree)
The first tree — the Note Tree — determines the current state of all data inside the system — smart contracts, registers of ownership of assets — everything. For now, let’s focus just on recording the ownership of assets through notes.
Suppose Alice sends Bob 50 zkDai and the Note Tree has slots 1, 2, … n filled up. Then the following is added to the Note Tree:
Encrypt (
{
owner: [Bob's Address], asset: 0x40a5a9872e73de550516d8ec43c6990f8247441d, amount: 50
}
)The Nullifier Tree
Locations in Tree = ~2²⁵⁶ leaves (sparse Merkle Tree)
The second tree — the Nullifier Tree — determines which notes have been spent — we add the following to the Nullifier Tree to mark Alice’s Input Note of 50 zkDai as spent.
Hash (
{
owner: [Alice's Address], asset: 0x40a5a9872e73de550516d8ec43c6990f8247441d, amount: 50
}
)
The ‘random’ nature of the Hash means the note in the nullifier set can’t be traced to the newly-added note in the Note Tree.
Sparse vs Dense (for enthusiasts)
The two-tree diagram above is actually slightly misleading in one respect — it shows the spent note being added to position 3 (out of 4) in the Nullifier Tree, at the same location it was originally created in the Note Tree.
However, these two trees have significantly different structures.
The Note Tree is actually encoded as a ‘dense’ Merkle Tree — that is, a tree designed to hold ~2³⁰ notes, and therefore requiring 30 hashes to add a note. You add the notes in the order in which they are created over the lifetime of the asset— first note at position 1, second note at position 2, etc. This tree is ‘dense’ because leaves are all created as immediate next-door neighbours.
The Nullifier Tree, however, looks very different — addresses, instead of running in order, are determined by the hash of the nullifier note data (detailed above). This of of course means that the Nullifier Tree is a sparse Merkle tree — that is, a tree with 2²⁵⁶ theoretically-available leaves — each containing the number 0. The note is added at the address determined by that hash — that’s right, the note hash’s value *also* doubles as its location in the tree. In other words, the Nullifier Note is placed into the Nullifier Tree amid a wilderness of zeros.
Notice that this means that the position of a note in the Nullifier Tree (i.e. being marked as spent) is ≠ the position in the Note Tree.
There are two excellent reasons for this:
- Privacy: No observer can connect the creation of a new note in the Note Tree with a note marked as ‘spent’ by being added to the Nullifier Tree — they’re in totally different positions, and unlinkable — that’s very important for privacy.
- Checking a Note is Spent: When we need to work out whether a note has been spent or not, then by adding the ‘shared secret’ data and looking at the hash, we can tell whether there is a zero at that location, or a note. If the tree were a ‘dense’ tree, we’d have no idea where the note had ended up — we’d have to check the whole tree just in case. But in a sparse tree, the data of the note determines precisely its location in the Nullifier Tree. So we can quickly check if it’s in that tree, and therefore whether or not it’s spent, by checking just one location.
Observation: Even though the Nullifier Tree has 2²⁵⁶ locations, and therefore 256 hashes between a leaf and the Merkle Root, most of the locations always hold the default value 0 (i.e. most locations are unused). This allows us to get the number of hashes needing verification nearer to 30, rather than 256.
Counting the Cost of Hashes
The following computation is indicative only — AZTEC is actually going to use more SNARK-friendly hashes e.g. Pedersen commitments.
But to complete the exercise:
- Note Tree: 30 hashes to add a new output note
- Nullifier Tree: 30 hashes to add a note, marking it as spent
- Total: 60 Hashes
Each SHA-256 hash in PLONK requires ~27,000 gates for a 64 byte input, so 60 hashes consume ~1.6m gates. The actual smart-contract logic can often be run in a handful of gates — sometimes 10s, 100s, or 1,000s of gates depending on the smart contract in question.
That leaves hashing algorithms dominating > 99% of the computation. And that is why benchmarking SNARKs on hashing algorithms is the crucial barometer of speed.
Join the Team
We’re on the lookout for talented engineers and applied cryptographers. If joining our mission to bring scalable privacy to Ethereum excites you — get in touch with us at hello@aztecprotocol.com.
Join our Community