Leveraging the flexibility of zk-SNARKs to make private DeFi transactions cheap and easy
Aztec has been working hard to make general purpose zero-knowledge transactions as easy as possible, and rapid advancements in zk cryptography are helping to make those transactions as cheap as they are easy. In this post we want to describe a fundamental technology that helps us get there.
Tradeoffs in the Design of Proving Systems
In a zero knowledge proving system, two parties engage each other so that one can convince the other that some statement is true. One party, which we call a prover, would like to convince another party, a verifier, that they have some particular kind of information while sharing as little of that information as possible. This often breaks down cleanly into two phases: proof generation, and proof verification. Ideally, both of these would be fast and computationally efficient, but the reality is one often has to accept tradeoffs between the two. (In an absolute computational sense, proof construction is generally more expensive than verification, thus when we talk about, for example, ‘fast’ construction, we mean relative to some meaningful baseline, not relative to verification).
In the setting of Aztec’s zk-rollup, there are actually three distinct parties engaging in the creation and verification of SNARK proofs, each with different computational powers and constraints:
- User: the user possesses secret information, such as their balances and their transaction history, which they would like to keep secret while still engaging in transactions and interactions with DeFi protocols. They generate proofs in a web browser, typically on a low-power device such as a phone.
- Rollup Provider: the rollup provider batches together and compresses user transactions, a process that involves proof generation as well as proof verification, at least in a sense (see more on recursion below). They generally have access to commercial grade hardware.
- Blockchain: the Ethereum Virtual Machine (EVM) is a highly-constrained computational environment where every operation has a varying, but typically expensive, cost that must be paid by the users in transaction fees. The EVM is responsible for verifying one proof (which encapsulates many other proofs).
To bring affordable, truly zero knowledge transactions to Aztec’s users, we blend together different proving systems (different, tasty flavors of PlonK, in particular) across recursion boundaries. For users, this means reduced computational cost during client-side proof generation, as well as reduced monetary cost through minimized computation on the EVM.
Recursion
Recursion is based on the following powerful observation: the verification of a zero knowledge proof is itself a computation that can be attested to by a zero knowledge proof. Said differently, there is nothing stopping us from replacing the action of verifying a SNARK proof p with a proof p* that p has been verified correctly. Of course, by doing this we have introduced p* which itself must be verified. But this starts to suggest a notion for how two different proving systems might be combined or ‘composed’.
Let’s view a proving system as a pair of algorithms (P, V), a prover and a verifier. Suppose we have one proving system, (P, V), which has cheap proof construction but expensive proof verification, and another, (P*, V*), which has expensive construction and cheap verification. Is there a way to compose them and reap the benefits of both? Consider the following process:
- Construct a proof under proving system P
- Construct * under proving system P*, where p* is a proof that attests to the correct verification of under V
- Verify *.
Ultimately, the benefit here is derived from the fact that each of these three steps can be performed by parties with different computational capabilities. A version of this idea is exactly what enables Aztec Connect to make cheap, private transactions available to its users. The two proving systems in question there are PlonK and TurboPlonK, where the former has cheap verification and the latter has efficient proof construction. A simplified outline of how we use this composition technique in our rollup is as follows:
- The Client constructs a proof –Client using TurboPlonK, a varietal of PlonK with custom gates (more on that below) to allow for efficient proof generation on constrained devices. They send –Client to the Rollup Provider.
- The Rollup Provider takes in –Client and constructs a Standard (i.e. non-Turbo) PlonK proof –Rollup that –Client has been verified correctly. In this sense, the Rollup Provider has been constrained by the high cost of TurboPlonK verification and Standard PlonK proof construction. But the rollup provider is mighty, and can handle both while still making money and creating massive savings for users. The proof –Rollup is sent to Ethereum.
- The EVM verifies –Rollup via a smart contract StandardVerifier.sol deployed to Ethereum.
Note: to further optimize the compression process, an Aztec rollup provider actually engages in three steps of recursion, two Turbo-to-Turbo (using the rollup and root rollup circuits, assembled in a way explained here) and one Turbo-to-Standard (the root verifier circuit).
Interlude for Nerds: Custom Gates
We want to illustrate, in a contrived, baby case, where the tradeoffs between Turbo and Standard PlonK come from. Our goal is to blackbox cryptographic concepts as much as possible, but the reader is warned that we get just a bit technical here.
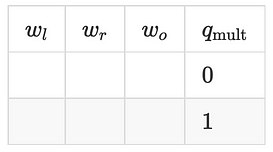
Scenario: you work as a protocol designer for a company called JazzTec. You have designed and implemented a zero knowledge proving system called PlunK that allows users to prove statements that include combinations of multiplication and addition like a + b = c, (a + b) · c = d, a · b · c = d, and so on. Your small proving system contains only one kind of gate, written symbolically as

Here the w represent “wires” with l = left, r = right, and o = output, and q is a “selector” that is used to switch between multiplication and addition. JazzTec’s circuit writers have made an app where a user (or prover) must show that they have found numbers a, b, c, and d such that

The circuit writers provide the users a template:
Schematically, the circuit looks like this:
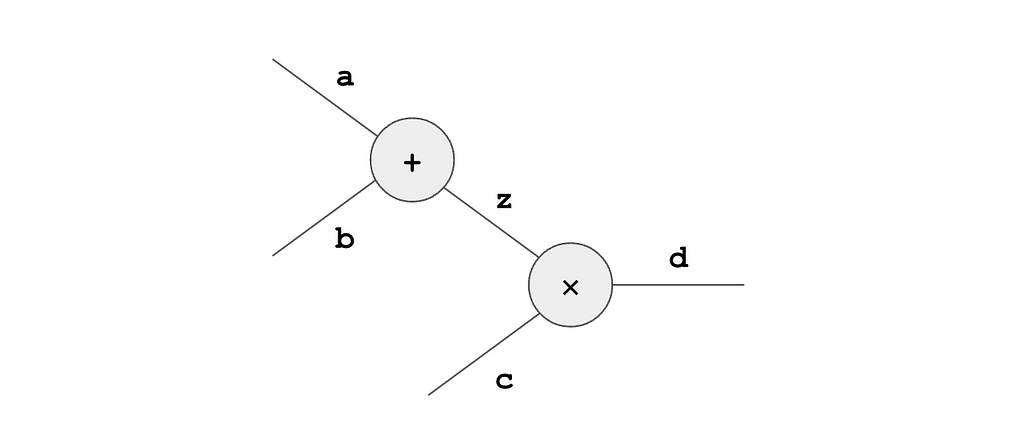
By filling in the template with values a, b, z, c and d like this:

the user can prove knowledge of values that satisfy the claim. (Well, almost. We’re ignoring the fact that a link must be enforced between the two instances of z. This relates to the notion of copy constraints, which is very important in general but not essential for making our present point).
After using PlunK for a while, JazzTec has decided to add a new feature which will require users to prove statements of the form x⁵ = y. (This is perhaps not such a made-up example. The recently developed Poseidon hash, for example, designed specifically for zero-knowledge proving systems, requires computation of fifth powers). How can we implement this type of operation using PlunK? Well, our expression can be decomposed into a series of multiplications and one addition as

Thus, the piece of the circuit designed to handle this operation might look like this:

With this new component added to the circuit template, an execution trace could look like this:

Now let’s consider an alternative approach. What if instead of using the more minimalistic setup of PlunK, we extend the proving system to one with native support for statements of the form x⁵ = y. The key idea here is that the circuit writer, who dictates to the prover the form of the statement to be proven, can add a new selector that introduces an additional interpretation for each row in the execution trace. Let’s flesh this out.
We’ll call our new, extended proving system TangoPlunK. It contains a new custom selector, and its generic gate has the form
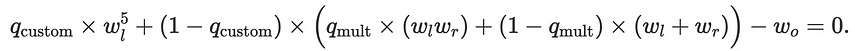
We see that the new q-custom selector switches on or off the custom functionality; when q-custom is 1, we have our fifth-power equation, and when q-custom is 0, we have the old standard PlunK equation. The operations involved in x⁵ = y can now be encapsulated into a single gate that looks like this

Using TangoPlunK, the execution trace for our program would simply be

To summarize, what used to take 6 gates now takes 3, so we have realized a 50% reduction in circuit size by switching to TangoPlunK!
A Quick Caveat for TurboNerds
The experienced reader might have noticed that introducing a custom gate for handling fifth-power type operations also increases the degree of the identity to be proven. In general, this can mean an increase in computational work for the prover, potentially counteracting some of the benefit gained from a reduction in circuit size. In our toy example, the degree of the identity doubled (from 3 with PlunK to 6 with TangoPlunK) but the size of the full circuit was halved (coincidentally, from 6 to 3). If our program contained a smaller proportion of computations representable by our custom gate, we’d have to reconsider its utility. In practice, such tradeoffs have to be taken into account.
It’s also important to note that one can conceive of useful custom gates that do not increase the degree of the identity, or at least not to the point where the prover feels the effect. This is the case, for example, in the original TurboPlonK proving system, where the critical innovation is the introduction of custom gates that facilitate efficient elliptic curve scalar multiplications in the context of computing Pedersen hashes.
Prover and Verifier Costs
Our example of PlunK and TangoPlunK is meant to highlight how computational tradeoffs can be made in the design of a proving system based on the observation that (1) prover complexity is fundamentally tied to the number of gates in the circuit, and (2) verifier complexity is relatively independent of circuit size but increases with the complexity of the claim or identity being proven.
For our sample program, TangoPlunK proof construction is cheap because the introduction of our custom gate allows for a substantial reduction in circuit size. Verification is relatively expensive in TangoPlunk because not only does the verifier see no benefit from the reduced circuit size, it must contend with a an identity that has increased in complexity relative to PlunK.
More concretely, in proving systems such as PlonK, a large portion of the computational cost for both the prover and the verifier is incurred through the need to compute expensive elliptic curve scalar multiplications. For the prover, these operations arise from the need to compute polynomial commitments in the construction of a proof . The number of scalar multiplications that need to be performed is proportional to the degree of the polynomials being committed to, which is in turn proportional to the number of gates in the circuit. (For those not familiar with the important role that polynomials play in SNARKs, we suggest this blog post by Vitalik Buterin).
For the verifier, on the other hand, scalar multiplications are primarily required in reconstructing the original claim or identity using the commitments received from the prover in . In particular, an additional selector in the identity directly results in an additional scalar multiplication during verification. Take a look, for example, at Step 9 from the Standard PlonK verification algorithm:

The q’s in this expression are the selectors of Standard PlonK, and the operation “·” represents elliptic curve scalar multiplication. With more selectors, this lovely expression gets even lovelier .
The example for nerds illustrates this tradeoff: In comparison with standard PlunK, TangoPlunK allows for a 50% reduction in the number of gates, lessening prover cost (at least in terms of commitments), while increasing the verifier complexity (via addition of the selector q-custom).
Of course, the reality we’re alluding to with this example is the similar tradeoff between the Standard PlonK proving system and TurboPlonK. That’s why in our applications at Aztec, like Aztec Connect, we arrange for the prover to use TurboPlonK and for the verifier to use Standard PlonK.
Going further
Zero knowledge cryptography has seen an explosion of activity in the past few years. At Aztec, we’re upgrading from TurboPlonK to what we call UltraPlonK, which is simply TurboPlonK + Plookup, a protocol we designed for using lookup tables to further speed up proof construction at additional cost to the verifier. At the opposite extreme, we’ve designed a protocol called Fflonk that allows extremely efficient verification at additional cost to the prover. Fflonk, which harnesses the commitment scheme of this paper (which we call SHPLONK), has the potential to reduce our EVM execution costs by 35%.
Conclusion
Zero knowledge proofs are an extremely cool, cutting-edge concept with enormous technological potential. What we describe here will be considered baby steps in harnessing that potential to create a better internet. Thanks for joining us on the way there!
Thanks to Jon Wu, Ariel Gabizon, Suyash Bagad, Innokentii Sennovskii and Guillaume Drevon for helpful comments and discussion.





