Advanced Version
Switch to Based Version
Approach
We’ll first explain how AZTEC Notes get validated — in other words, how our range proof works.
That should help explain why we need a ceremony — in particular, why we require a register of points known as the AZTEC Codex.
References
Motivation
AZTEC’s Core Transaction is a confidential UTXO — given an input note of size k₁ we wish to spend money by generating output notes size k₂ and k₃ — for example, k₂ might be the amount you’re sending a counterparty, and k₃ may be the spare change you want to keep.
- k₁ = k₂ + k₃ —encryption via sigma protocols allows this to be easily checked — details in our White Paper
- k₂ and k₃ are both within a fixed range, and therefore the wrap-around attack (e.g. 10 = 11 + -1) is not available to the attacker
To achieve (2), the range proof, AZTEC instead deploys a proof of set membership — i.e. that the encrypted forms of k₂ and k₃ sit inside a proscribed set 1, 2, 3, …, Max.
How to Prove (2) — the Range Proof
AZTEC’s range proof extends a set membership technique of Camenish et al, using Boneh-Boyen signatures.
Suppose, somehow, there exists a register of encrypted numbers k, of the following form:

Note that to the observer these are just points — they can’t explicitly ‘see’ y. So it’s nice to rewrite these as:
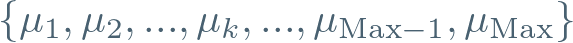
Suppose further that another generator g₂ is raised to the power of y, and that the result of this has been published somewhere for all to see:

Well, it turns out that there’s a clever construction allowing a prover / spender to ‘wrap’ one of these numbers (we call this a ‘note’), and prove to a third party that either he / she knows the number y, or else that the note was formed from this register — in other words, that the number j is in the range.
This construction requires a fresh random number v (the viewing key) for each note, and is formed as follows:
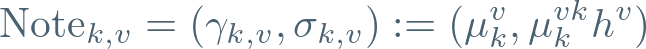
Note that this can be formed without knowledge of y. But magically, we have constructed two points with a special relationship — the right-hand argument can be rewritten as follows:
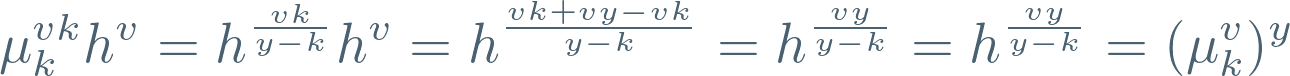
So, we’ve got a pair of points related by y.
Now, recall that an elliptic curve pairing allows ‘ratios’ of exponents to be compared — well, let’s haul in that Reference Point, and check:
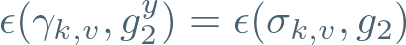
If this is true, what can we deduce?
Well, either:
- The spender had access to y, or
- The spender must have used one of the points from the AZTEC shelf (codex) — otherwise, generating a ‘ratio’ of y between these points would have been impossible
We need to stop (1) being an option.
That’s where the AZTEC Ceremony comes in — to avoid y ever being explicitly created.
The Mathematics of the Ceremony
We know what we need to do — we need to build that Codex of points, without y ever being explicitly constructed.
As a reminder, we need to construct Boneh-Boyen signatures for each k as follows:
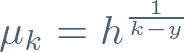
Here’s the first observation — those Boneh-Boyen signatures are just expressions in y. How could we construct this not knowing y? Well, we can certainly do it if we know the following ‘monomials’ in y:
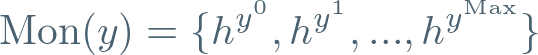
If we could construct these, then the task of building that Codex is pretty simple — define two polynomials (we’ll be evaluating both of these at y):
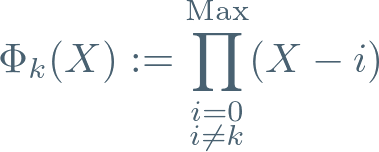
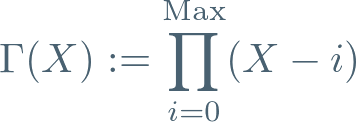
Now notice that we can divide these to get:

In other words, we can find the k’th point of the Codex with the following computation:
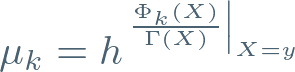
And even better, we can do it without ever knowing y.
How?
Well, we just need to know Mon(y) (i.e. the monomials evaluated as elliptic curve points) and then compute all those coefficients — expensive and painful, yes.
But we only need to go through this once.
A Rotation Trick
Dividing in elliptic curve world is pretty hard work.
So here’s a trick. Let’s actually do everything base g, and then define h as:

We’ve essentially rotated the whole curve around by a factor of Γ(y), to avoid a nasty division!
Those Monomials — How Did You Make Them?
Fortunately, that’s the simplest bit of all — we have a relay.
Participant 1 takes the generator point h (computed from g as already seen), and then generates some toxic information z₁. Finally, they form Transcript 1 as follows:

Next, Participant 2 receives these points and rolls in their toxic information to form:

Note that Participant 2 does this just by exponentiating Participant 1’s points — never knowing what number z₁ was used to form them.
If there are (say) 100 participants, then the number y is in fact:

But, unless every single participant colluded with its neighbours, this number will never be known .
And We’re Done
Now to reattach names to the maths:
- The Relay — The process of forming Mon(y) by producing the Transcripts one after the next
- Post Processing — The process of computing those coefficients, and working out the Codex of Boneh Boyen signatures
So now you know what’s going on under the hood — please sign up!






