Our previous article about AZTEC described how the protocol works, but I left the ‘why’ part for another day, so hello there!

This article is an in-depth look into how the AZTEC protocol enables efficient confidential transactions.

But before I start, I have a confession to make.

You see, I have a problem when it comes to explaining cryptography. It is in general quite confusing and unintuitive — the practise of proving you know relationships between data without having to share what that data is. It’s a little odd, and difficult to explain.

This problem isn’t something I alone struggle with. If you ever read cryptographic papers or articles, the author will usually attempt to translate these odd concepts into something more intuitive and familiar by wheeling out Alice and Bob.

Alice and Bob are the world’s most uninspiring double act and they only have one routine. When Alice and Bob turn up, they will immediately begin to embark on an abstract series of guessing games with seemingly arbitrary rules. Sometimes Alice or Bob don’t know some of the rules, which clears up precisely nothing. This game usually takes place in a cave and Alice might have some coins (public coins). You know you’re really in for a treat when Bob begins to monologue about how a uniformly distributed random number generator can be distinguished from a hash function.

I do not like Alice and Bob. I find their presence to be unhelpful. Still, as I have not managed to square the circle of intuitively explaining zero knowledge proofs I have invoked them in this article but I want to make one thing clear; I’m not happy about it.

{{blog_divider}}

Dissecting a confidential transaction

Before describing what the protocol does, I want to start with what we need so that when I introduce a concept I can explain why it has value. We want a way of representing ‘balances’ with encrypted numbers. E.g. instead of a ledger recording that I have 20 Ethereum and that you have 5, these numbers are encrypted.

We can’t record this as a simple encrypted ledger, because if I want to send you money, I would need to be able to figure out what your new encrypted balance should be — but I don’t know your original balance so this is hard to do.

So instead of mapping owners to balances, we map balances to owners via the concept of an encrypted ‘note’.

• A note is worth some defined amount and has an owner.
• If I own multiple notes, I can combine them into a single note.
• If I own a note, I can split it into multiple notes. These notes can have different owners

I can transfer ‘value’ by splitting a note and having one (or more) notes owned by the recipient.

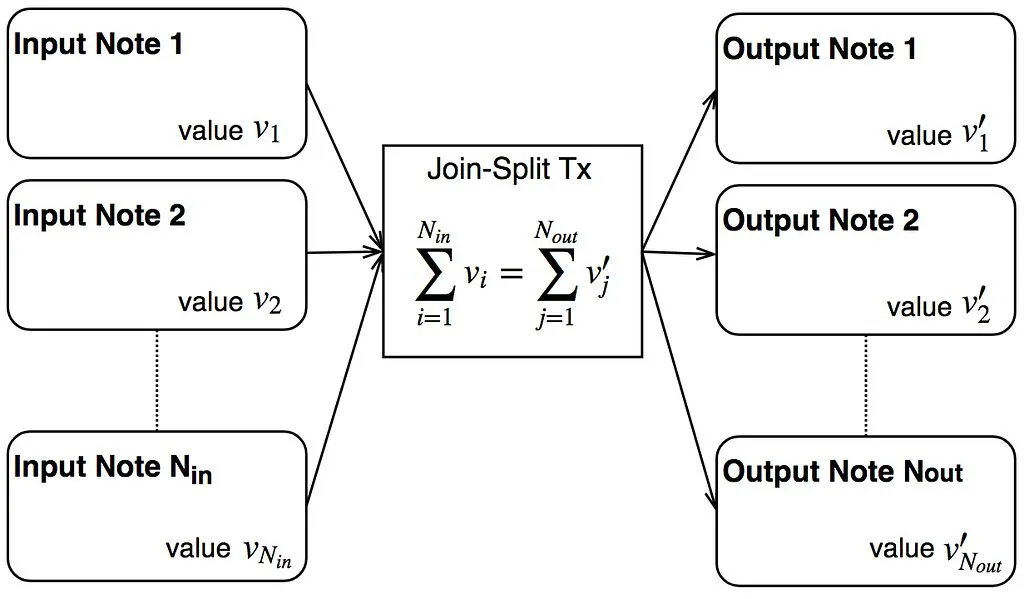
In the world of encrypted notes, what do we need for a confidential transaction?

• A way of encrypting value into notes
• A way of proving that the sum of the values of some input notes, equal the sum of the values of some output notes

And in order to get those things, we need to dive into the world of elliptic curve cryptography.

{{blog_divider}}

Elliptic curve cryptography and homomorphic encryption

Elliptic curves have relatively simple formulae, for example the curve we use has the formula y² = x³ + 3 (the 3 is important…). If drawn on a piece of paper, we can pretend it looks like this:

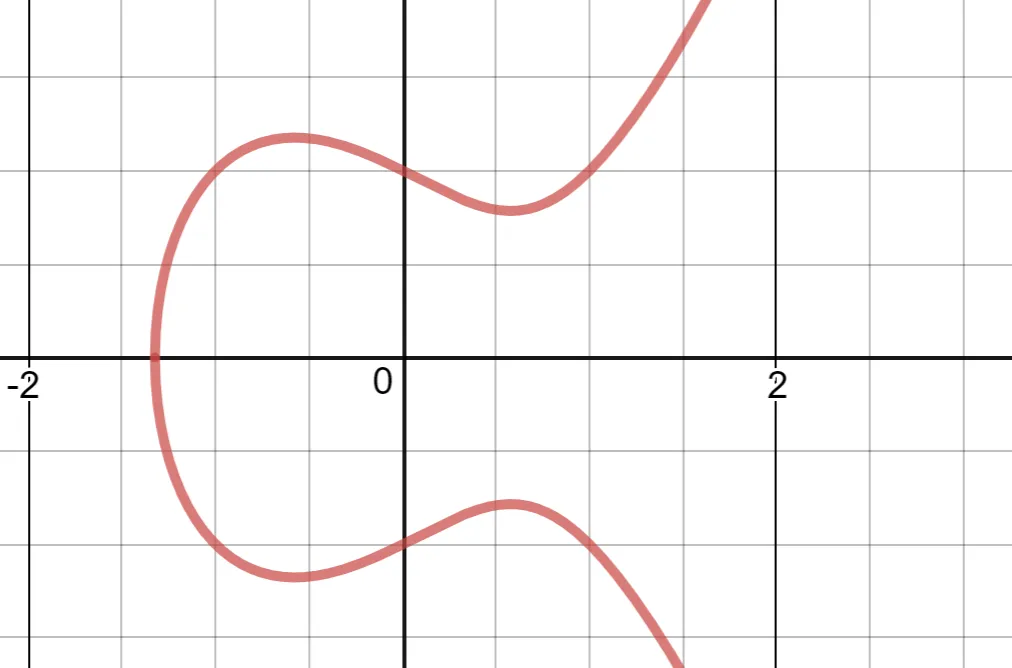
We use elliptic curves because they can be used to create one-way functions (can map from A → B, but if given B you can’t figure out A) that preserve some mathematical operations.

Here’s how it works. If you have two points on a curve, draw a line through them and find where that line hits the curve for the 3rd time (which will always happen), then invert that point in the y-axis. The resulting point is the result of our ‘addition’ operation.

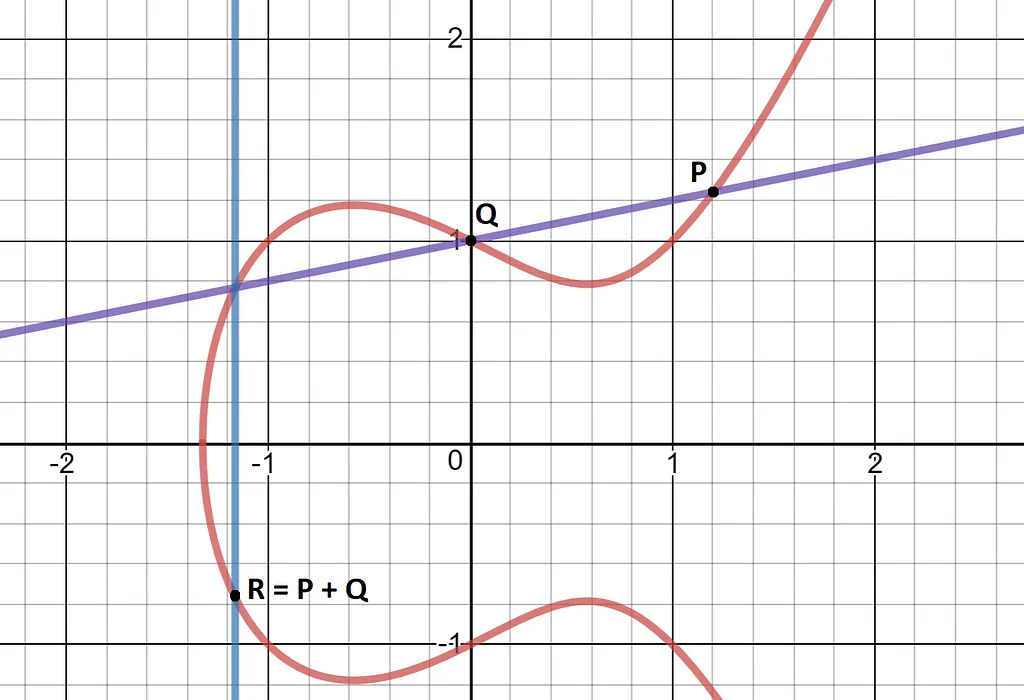
When adding a point to itself, the line that’s drawn is the tangent to the curve at that point.

We require the inversion in the y-axis because without out it our ‘addition’ is not associative: (P+Q) + R would not equal P+ (Q+R).

But…why?

Good question! We can use point addition to define elliptic curve scalar multiplication. If we have a point, P, and an integer x, we can ‘multiply’ P by x, but adding P to itself x times.

If the elliptic curve parameters are carefully chosen, scalar multiplication is a one-way function. If I have x and P, I can easily compute x•P. But if I have P and x•P, I can’t figure out x. Naturally, terms and conditions apply. This only works if x is a random number, or has randomness added into it (if x is predictable then it’s much easier to figure it out via trial-and-error brute force techniques).

But…why?

Good question! There are cheaper and faster one-way functions out there, like hashing algorithms. But elliptic curves preserve some of the mathematical properties of the values they encrypt.

Take two random integers x and y and calculate x•G and y•G. Now add them together. The resulting point is the same point you get by adding together x and y, then multiplying the result by G.

‍P = x•G + y•G = (x+y)•G

‍This ability to perform homomorphic addition means we can perform additions on encrypted numbers as if they weren’t encrypted, which is rather useful.

Naturally, terms and conditions apply. The problem (well, one of them) with homomorphic addition over elliptic curves is that the addition is performed modulo an extremely large prime number p. For the curve we use, this is equal to 21888242871839275222246405745257275088548364400416034343698204186575808495617.

Imagine we want to validate a ‘transaction’. I have a note worth 0 and I want to convert it into a note worth -1 and 1. Let’s represent these values as ‘notes’ on an elliptic curve: -1•G and 1•G.

Naturally, 0•G = -1•G + 1•G. So we can satisfy the balancing relationship required by our join-split transaction. But for our elliptic curve, -1 is actually p-1, which is a huge number!

If we used this kind of logic to validate dollar-denominated confidential transactions, we have just created a ‘note’ worth more dollars than the amount that exists in the observable universe, which is a bit of a problem.

{{blog_divider}}

Range proofs to the rescue

We need a range proof to deal with this problem. If we check that every encrypted number that enters our cryptosystem is many orders of magnitude less than p/2, then it’s never possible to ‘wrap’ around the modulus boundary and create ‘negative’ numbers.

But we have another problem now. If the modular nature of homomorphic arithmetic is the villain in our story, then range proofs are less of a plucky hero with heart and plot armor, and more like a cut-throat mercenary who will pillage everything down to the elastic in your pants. Range proofs are expensive. The computational cost to verify most range proofs adds a significant overhead to the cryptographic protocols that use them.

For example, a common method is to create encrypted representations of every bit in a number, and then prove that every bit is either 0 or 1. However for, say, a 32-bit number, you would need to validate 32 zero-knowledge proofs. There are some ingenious techniques for squishing the size of these proofs down and combining them into a mega-proof, but the amount of computation required by a verification program will still scale with the number of bits your encrypted number can potentially contain.

For the Ethereum protocol, this translates into gas costs that quickly hit the block gas limit.

{{blog_divider}}

Range proofs via digital signatures

Picture the scene. You are a proud and loyal citizen of the People’s Representative Democratic Party of Zero-Knowledgeandia. In this timeline, you are called Alice due to a clerical incident at the registry office; the Party does not make mistakes.

Today, you are stoically queuing at the bread line in order to feed your family for another week.

However, you have a problem. Commissar Bob will only sell bread to upstanding citizens who have a sufficiently low State Disobedience score.

Naturally, you are a proud and loyal citizen and do in fact posess a sufficiently low score. However if you simply tell Bob your score you will be sentenced to 5 years of hard labour in the acid-boron caves for not being GDPR-2.0 compilant.

Your one saving grace is that Bob, being a stickler for following rules, absolutely loves abstract guessing games with public coins. So you can use a zero-knowledge proof.

However, Bob only posesses an 8-bit Robotron-1999 People’s Tabulating Machine and only has one minute to process your proof before you get kicked out of the bread line for loitering.

How can Alice present Bob with an efficient range proof that her score is below a threshold? Will Alice’s family be fed for another week?

It is on this cliff-hanger that we will dive into the depths of the AZTEC protocol and its range proof.

{{blog_divider}}

Saving the day with lazy range proofs

In software engineering we have a principle called lazy evaluation. Simply put, don’t bother doing something unless you have to, and only do it when you need to. It might be expensive to verify a range proof, but it is much cheaper to verify that somebody else has verified a range proof.

Digital Signatures and range proofs

Making range proofs somebody else’s problem introduces a trusted setup into the protocol, performed by the “somebody else” in question. In this setup phase, we generate a random integer y, the trusted setup private key (this is the ‘toxic waste’ of our protocol). The trusted setup public key is published (y•G), along with digital signatures for every integer that we tolerate in our range proof (e.g. 0 to 1 million). Once this is done, knowledge of y must be destroyed.

Now, in order to perform a range proof, all we need to do is present a signature, and prove it was signed by y. If we have done our job properly, this means that the integer in the signature is also inside the allowed range, because those were the only signatures that were created.

This does introduce risk that y is not destroyed and information about it is leaked. However we have a multiparty computation protocol that enables our trusted setup to be performed by a large number of people (ideally thousands). Each person generates their own piece of ‘toxic waste’, performs their part of the computation, then destroys their waste. Only one person has to act honestly and destroy their toxic waste for the entire protocol to be secure.

With out of the way, here, hold these:

The point μ is a form of Bohen-Boyen (BB) signature and is part of the trusted setup signature database. The integer k represents a number that we accept in our range proof, so we have one signature for each integer in our range. The integer y represents a special trusted-setup private key and the point T represents the trusted-setup public key.

If we are given a point μ and a scalar k, we can check whether μ is indeed a signature without knowing what y is; we only need T.

Why is this? Well, our tactic is to embed the ratio G: y•G into the encryption of every number in the range register, so in a way that is somehow testable but also irrecoverable. Bilinear parings test ratios of exponents and enable us to blinding, magically, test that our ‘signature’ cam from a pre-constructed list signed by y (we can ‘fake’ a proof this proof by knowing y, which is why it is paramount that knowledge of y is destroyed).

We know the values of G and y•G. If we also can get μ and y•μ, we can validate that the mapping between (G -> y•G) and (μ ->y•μ) is the same and therefore we can prove that μ is a signature from the signature database. This is what we require for our bilinear pairing comparison.

In order to do this, we need y•μ. To get this, we need to compute this quantity:

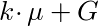
This might make more sense if we re-write G as ((y -k)/(y-k))•G, and μ in terms of G:

Because of homomorphic addition, the ‘scalar multiplier’ of G is y/(y-k), leading us to this:

Validating Boneh-Boyen signatures: bilinear pairings

For any valid Boneh-Boyen signature μ, we can compute y•μ despite not knowing the value of y. But how do we know that this signature was signed by the trusted setup private key and is not a forgery?

If we have these two points, we can check that y is indeed the correct private key through a bilinear pairing.

Vitalik wrote a great article on bilinear pairings that explains it better than I can, if you want to know more I recommend reading it. To summarise, pairings perform a kind of multiplication of elliptic curve points. If I perform the pairing operation on two points: e(a•P,b•R), it doesn’t matter which points contain the scalars a and b because the result multiplies them together. For example, the following four pairing operations create the same result:

‍e(a•P,b•R) = e(b•P,a•R) = e(ab•P,R) = e(P,ab•R)

‍So take our trusted-setup public key, T = y•G. If we are given elliptic curve points μ and y•μ, we can check that this is the case by pairing these points with T and G respectively and checking both sides of the following equation match:

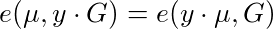
Putting it all together, we can validate whether an elliptic curve point μ is a Boneh-Boyen signature over an integer k, signed by trusted-setup private key y, by validating the following equation:

The takeaway from this, is that if a person can prove that they have a signature signed by y, and link the value k of the signature to an encrypted value, then we know that the encrypted value can only be one of the integers signed in the trusted setup. I.e. we have a range proof. Tadaaa…

It’s important that this can be done without anybody actually knowing what yis, because y was destroyed at the end of the trusted setup process.

The value in all of this is that the verification equation does not care about how big k is. The bigger the range, the bigger the signature database created by the trusted setup, but the computational cost of verifying this range proof is always constant.

But wait, there’s more! Creating an encryption scheme with an embedded range proof

During our trusted setup protocol, we created an elliptic curve point μ for every integer we accept in our range proof and put them in a database. We also publish the public key T.

‍So now, we can pick out one of these points and prove that it was signed by T. But this does not give us the confidentiality we need.

If I see somebody else use a signature point in a transaction, I can just look up which integer that point corresponds to in the database!

We need to add in a randomizing factor. Pick a random variable a. This is our viewing key. Now, if we want to construct a range proof over an integer k, we pick out the required point μ and multiply it by the viewing key. Let’s call this point γ

In order to prove that γ is a signature signed by y, we need to be able to get y•γ. instead of y•μ. But this is straightforward, just compute k•γ + a•G instead of k•μ + G:

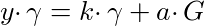
Let’s introduce a point, σ, to represent this: σ = y•γ. Now, to prove we have a valid signature given the pair of points (γ, σ), a verifier must validate that the following equations are true:

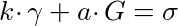
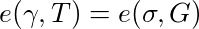
The value in this is that an observer cannot link γ to a signature in the signature database, because we’ve scrambled the signature with our viewing key a. However, we can still prove that whatever γ contains, it is still a Boneh-Boyen signature signed by the trusted setup private key y, even though nobody actually knows what this is and all we have to work with is T.

{{blog_divider}}

Putting it all together: the AZTEC ‘commitment’ function

You might have noticed that this bilinear pairing verification equation requires the integers k and a. The verification equations are being run inside a ‘smart contract’ validation algorithm, and we naturally don’t want to broadcast these integers! That’s kind of the whole point.

This is relatively straightforward and can be done through a zero-knowledge proof. But that is a whole other article in and of itself, for now let’s just assume this can be done.

The two points (γ, σ) represent an encryption of an integer k. Given these two points, only one specific value of k and one specific value of a will satisfy the verification equations.

This is because γ is a function of the trusted setup private key y, and the generator point G is not. Assuming the trusted setup is done properly, and knowledge of y has been destroyed, it is not possible to ‘factorize’ out the integer (k) multiplying γ, by adding terms to the integer (a) multiplying G, without breaking elliptic curve cryptography.This is the computational binding property that is required for a useable encryption scheme.

It is also not possible to glean any information about k by examining the points (γ, σ), other than the fact that it is within our range proof bounds. This is because the viewing key (a) acts as a randomizing factor that needs to be factored out before k can be extracted. This is the perfectly hiding property, the second property required for any encryption scheme.

Naturally, if I give you an encrypted point pair (γ, σ) and the viewing key (a), you can figure out what k is (I mean, it’s called a viewing key for a reason!). This is because we can compute k•γ by computing σ — a•G. Now that we have k•γ and γ, we can extract k via a brute-force algorithm (because the set of integers that k is from is relatively small, say between a million and a billion values).

It is this commitment function, an encryption scheme that contains an implicit range proof, that enables the AZTEC protocol’s zero-knowledge proofs to be efficiently verified.

Well, that’s about it for now. Over the coming weeks we’ll be publishing more articles about the workings of the AZTEC protocol, as this one only scratches the surface. If you want to learn more, you can read a complete description of the AZTEC protocol and its soundness properties in our paper.

Cheers,

Zac.