
Hello there!
I want to write about a piece of runoff that has oozed out of the primordial slop on the AZTEC factory floor: …Huff.
Huff is an Ethereum smart contract programming ‘language’ that was developed while writing weierstrudel, an elliptic curve arithmetic library for validating zero-knowledge proofs.
Elliptic curve arithmetic is computationally expensive, so developing an efficient implementation was paramount, and not something that could be done in native Solidity.
It wasn’t even something that could be done in Solidity inline assembly, so we made Huff.
To call Huff a language is being generous — it’s about as close as one can get to EVM assembly code, with a few bits of syntactic sugar bolted on.
Huff programs are composed of macros, where each macro in turn is composed of a combination of more macros and EVM assembly opcodes. When a macro is invoked, template parameters can be supplied to the macro, which themselves are macros.
Unlike a LISP-like language or something with sensible semantics, Huff doesn’t really have expressions either. That would require things like knowing how many variables a Huff macro adds to the stack at compile time, or expecting a Huff macro to not occasionally jump into the middle of another macro. Or assuming a Huff macro won’t completely mangle the program counter by mapping variables to jump destinations in a lookup table. You know, completely unreasonable expectations.
Huff doesn’t have functions. Huff doesn’t even have variables, only macros.
Huff is good for one thing, though, which is writing extremely gas-optimised code.
The kind of code where the overhead of the jump instruction in a function call is too expensive.
The kind of code where an extra swap instruction for a variable assignment is an outrageous luxury.
At the very least, it does this quite well. The weierstrudel library performs elliptic curve multiple-scalar multiplication for less gas than the Ethereum’s “precompile” smart contract. An analogous Solidity smart contract is ~30–100 times more expensive.
It also enables complicated algorithms to be broken down into constituent macros that can be rigorously tested, which is useful.
Huff is also a game, played on a chess-board. One player has chess pieces, the other draughts pieces. The rules don’t make any sense, the game is deliberately confusing and it is an almost mathematical certainty that the draughts player will lose. You won’t find references to this game online because it was “invented” in a pub by some colleagues of mine in a past career and promptly forgotten about for being a terrible game.
I found that writing Huff macros invoked similar emotions to playing Huff, hence the name.
Programming in Huff
Given the absence of any documentation, I figured it might be illuminating to write a short series in how to write a smart contract in Huff. You know, if you’re looking for time to kill and you’ve run out of more interesting things to do like watch paint dry or rub salt in your eyes.
If you want to investigate further, you’ll find Huff on GitHub. For some demonstration Huff code, the weierstrudel smart contract is written entirely in Huff.
“Hello World” — an ERC20 implementation in Huff
Picture the scene — the year is 2020 and the world is reeling from a new global financial crisis. With the collapse of the monetary base, capital flees to the only store of stable value that can be found — first-generation Crypto-Kitties. Amidst this global carnage, Ethereum has failed to achieve its scaling milestones and soaring gas fees cripple the network.
It is a world on the brink, where one single edict is etched into the minds citizens from San Francisco to Shanghai — The tokens must flow…or else.
This is truly the darkest timeline, and in the darkest timeline, we code in Huff.
Finding our feet
We’re going to write an ERC20 token contract. But not just any ERC20 contract— we’re going to write an ERC20 contract where every opcode must justify its place, or be scourged from existence…
Let’s start by looking at the Solidity interface for a ‘mintable’ token — there’s not much point in an ERC20 contract if it doesn’t have any tokens, after all.
function totalSupply() public view returns (uint); function balanceOf(address tokenOwner) public view returns (uint); function allowance(address tokenOwner, address spender) public view returns (uint); function transfer(address to, uint tokens) public returns (bool); function approve(address spender, uint tokens) public returns (bool); function transferFrom(address from, address to, uint tokens) public returns (bool); function mint(address to, uint tokens) public returns (bool);
event Transfer(address indexed from, address indexed to, uint tokens); event Approval(address indexed tokenOwner, address indexed spender, uint tokens);
That doesn’t look so bad, how hard can this be?
Bootstrapping
Before we start writing the main subroutines, remember that Huff doesn’t do variables. But there’s a macro for that! Specifically, we need to be able to identify storage locations with something that resembles a variable.
Let’s create some macros that refer to storage locations that we’re going to be storing the smart contract’s state in. For Solidity smart contracts, the compiler will (under the hood) assign every storage variable to a storage pointer and we’re doing the same here.
First up, the storage pointer that maps to token balances:
#define macro BALANCE_LOCATION = takes(0) returns(1) {
0x00
}
The takes field refers to how many EVM stack items this macro consumes. returns refers to how many EVM stack items this macro will add onto the stack.
Finally, the macro code is just 0x00 . This will push 0 onto the EVM stack; we’re associating balances with the first storage ‘slot’ in our smart contract.
We also need a storage location for the contract’s owner:
#define macro OWNER_LOCATION = takes(0) returns(0) {
0x01
}
Implementing SafeMath in Huff
SafeMath is a Solidity library that performs arithmetic operations whilst guarding against integer overflow and underflow.
We need the same functionality in Huff. After all, we wouldn’t want to write unsafe Huff code. That would be irrational.
ERC20 is a simple contract, so we will only need addition and subtraction capabilites.
Let’s consider our first macro, MATH__ADD . Normally, this would be a function with two variables as input arguments. But Huff doesn’t have functions.
Huff doesn’t have variables either.
…
Let’s take a step back then. What would this function look like if we were to rip out Solidity’s syntactic sugar? This is the function interface:
function add(uint256 a, uint256 b) internal view returns (uint256 c);
Under the hood, when the add function is called, variables a and b will be pushed to the front of the EVM’s stack.
Behind them on the stack will be a jump label that corresponds to the return destination of this function. But we’re going to ignore that — It’s cheaper to directly graft the function bytecode in-line when its needed, instead of spending gas by messing around with jumps.
So for our first macro, MATH__ADD , we expect first two variables to be at the front of the EVM stack; the variables that we want to add. This macro will consume these two variables, and return the result on the stack. If an integer overflow is triggered, the macro will throw an error.
Starting with the basics, if our stack state is: a, b , we need a+b . Once we have a+b , we need to compare it with either a or b . If either are greater than a+b, we have an integer overflow.
So step1: clone b , creating stack state: b, a, b . We do this with thedup2 opcode. We then call add , which eats the first two stack variables and spits out a+b , leaving us with (a+b), b on the stack.
Next up, we need to validate that a+b >= b. One slight problem here — the Ethereum Virtual Machine doesn’t have an opcode that maps to the >= operator! We only have gt and lt opcodes to work with.
We also have the eq opcode, so we could check whether a+b > band perform a logical OR operation with a+b = b . i.e.:
// stack state: (a+b) b dup2 dup2 gt // stack state: ((a+b) > b) (a+b) b dup3 dup3 eq // stack state: ((a+b) = b) ((a+b) > b) (a+b) b or // stack state: ((a+b) >= b) (a+b) b
But that’s expensive, we’ve more than doubled the work we’re doing! Each opcode in the above section is 3 gas so we’re chewing through 21 gas to compare two variables. This isn’t Solidity — this is Huff, and it’s time to haggle.
A cheaper alternative is to, instead, validate that (b > (a+b)) == 0 . i.e:
// stack state: (a+b) b dup1 dup3 gt // stack state: (a > (a+b)) (a+b) b iszero // stack state: (a > (a+b) == 0) (a+b) b
Much better, only 12 gas. We can almost live with that, but we’re not done bargaining.
We can optimize this further, because once we’ve performed this step, we don’t need bon the stack anymore — we can consume it. We still need (a+b)on the stack however, so we need a swap opcode to get b in front of (a+b) on the program stack. This won’t save us any gas up-front, but we’ll save ourselves an opcode later on in this macro.
dup1 swap2 gt // stack state: (b > (a+b)) (a+b) iszero // stack state: ((a+b) >= b) (a+b)
Finally, if a > (a+b) we need to throw an error. When implementing “if <x> throw an error”, we have two options to take, because of how thejumpi instruction works.
jumpi is how the EVM performs conditional branching. jumpi will consume the top two variables on the stack. It will treat the second variable as a position in the program’s program counter, and will jump to it only if the first variable is not zero.
When throwing errors, we can test for the error condition, and if true jump to a point in the program that will throw an error.
OR we can test for the opposite of the error condition, and if true, jump to a point in the program that skips over some code that throws an error.
For example, this is how we would program option 2 for our safe add macro:
// stack state: ((a+b) >= b) (a+b)
no_overflow jumpi
0x00 0x00 revert // throw an error
no_overflow:
// continue with algorithm
Option one, on the other hand, looks like this:
// stack state: ((a+b) >= b) (a+b) iszero // stack state: (b > (a+b)) (a+b) throw_error jumpi // continue with algorithm
For our use case, option 2 is more efficient, because if we chain option 2 with our condition test, we end up with:
dup2 add dup1 swap2 gt iszero iszero throw_error jumpi
We can remove the two iszero opcodes because they cancel each other out! Leaving us with the following macro
#define macro MATH__ADD = takes(2) returns(1) {
// stack state: a b
dup2 add
// stack state: (a+b) b
dup1 swap2 gt
// stack state: (a > (a+b)) (a+b)
throw_error jumpi
}
However, we have a problem! We haven’t defined our jump label throw_error , or what happens when we hit it. We can’t add it to the end of macro MATH__ADD , because then we would have to jump over the error-throwing code if the error condition was not met.
We would prefer not to have macros that use jump labels that are not declared inside the macro itself. We can solve this by passing the jump label throw_error as a template parameter. It is then the responsibility of the macro that invokes MATH__ADD to supply the correct jump label — which ideally should be a local jump label and not a global one.
Our final macro looks like this:
template <throw_error_jump_label>
#define macro MATH__ADD = takes(2) returns(1) {
// stack state: a b
dup2 add
// stack state: (a+b) a
dup1 swap2 gt
// stack state: (a > (a+b)) (a+b)
<throw_error_jump_label> jumpi
}
The jumpi opcode is 10 gas, and the others cost 3 gas (assuming <throw_error_jump_label> eventually will map to a PUSH opcode) — in total 28 gas.
As an aside — let’s consider the overhead created by Solidity when calling SafeMath.add(a, b)
First, values a and b are duplicated on the stack; functions don’t consume existing stack variables. Next, the return destination, that must be jumped to when the function finishes, is pushed onto the stack. Finally, the jump destination of SafeMath.add is pushed onto the stack and the jump instruction is called.
Once the function has finished its work, the jump instruction is called to jump back to the return destination. The values a , b are then assigned to local variables by identifying the location on the stack that these variables occupy, calling a swap opcode to manoeuvre the return value into the allocated stack location, followed by a pop opcode to remove the old value. This is performed twice for each variable. In total that’s…
- 4 dup opcodes (3 gas each)
- 2 jump opcodes (8 gas each)
- 2 swap opcodes (3 gas each)
- 2 pop opcodes (2 gas each)
- 2 jumpdest opcodes (1 gas each)
To summarise, the act of calling SafeMath.add as a Solidity function would cost 40 gas before the algorithm actually does any work.
To summarise the summary, our MATH__ADD macro does its job in almost half the gas it would cost to process a Solidity function overhead.
To summarise the summary of the summary, this is acceptable Huff code.
Subtraction
Finally, we need an equivalent macro for subtraction:
template <throw_error_jump_label>
#define macro MATH__SUB = takes(2) returns(1) {
// stack state: a b
// calling sub will create (a-b)
// if (b>a) we have integer underflow - throw an error
dup1 dup3 gt
// stack state: (b>a) a b
<throw_error_jump_label> jumpi
// stack state: a b
sub
// stack state: (a-b)
}
Utility macros
Next up, we need to define some utility macros we’ll be using . We need macros that validate that the transaction sender has not sent any ether to the smart contract, UTILS__NOT_PAYABLE. For our mint method, we’ll need a macro that validates that the message sender is the contract’s owner, UTILS__ONLY_OWNER:
template<error_location>
#define macro UTILS__NOT_PAYABLE = takes(0) returns(0) {
callvalue <error_location> jumpi
}
#define macro UTILS__ONLY_OWNER = takes(0) returns(0) {
OWNER_LOCATION() sload caller eq is_owner jumpi
0x00 0x00 revert
is_owner:
}
N.B. revert consumes two stack items. p x revert will take memory starting at x, and return the next p bytes as an error code. We’re not going to worry about error codes here, just throwing an error is good enough.
Creating the constructor
Now that we’ve set up our helper macros, we’re close to actually being able to write our smart contract methods. Congratulations on nearly reaching step 1!
To start with , we need a constructor. This is just another macro in Huff. Our constructor is very simple — we just need to record who the owner of the contract is. In Solidity it looks like this:
constructor() public {
owner = msg.sender;
}
And in Huff it looks like this:
#define macro ERC20 = takes(0) returns(0) {
caller OWNER_LOCATION() sstore
}
The EVM opcode caller will push the message sender’s address onto the stack.
We then push the storage slot we’ve reserved for the owner onto the stack.
Finally we call sstore, which will consume the first two stack items and store the 2nd stack item, using the value of the 1st stack item as the storage pointer.
For more information about storage pointers and how smart contracts manage state — Anreas Olofsson’s Solidity workshop on storage is a great read.
Parsing the function signature
Are we ready to start writing our smart contract methods yet? Of course not, this is Huff. Huff is efficient, but slow.
I like think of Huff like a trusty tortoise, if the tortoise is actually a hundred rats stitched into a tortoise suit, and each rat is a hundred maggots stitched into a rat suit.
…anyhow, we still need our function selector. But Huff doesn’t do functions; we’re going to have to create them from more basic building blocks.
One of the first pieces of code generated by the Solidity compiler is code to unpick the function signature. A function signature is a unique marker that maps to a function name.
For example, consider the solidity function
function balanceOf(address tokenOwner) public view returns (uint balance);
The function signature will take the core identifying information of the function:
- the function name
- the input argument types
This is represented as a string, i.e. “balanceOf(address)”. A keccak256 hash of this string is taken, and the most significant 4 bytes of the hash are then used as the function signature.
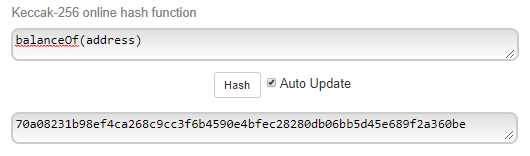
It’s a bit of a mouthful, but it creates a (mostly) unique identifier for any given function — this allows contracts to conform to a defined interface that other smart contracts can call.
For example, if the function signature for a given function varied from contract to contract, it would be impossible to have an ‘ERC20’ token, because other smart contracts wouldn’t know how to construct a given contract’s function signature.
With that out of the way, we will find the function signature in the first 4 bytes of calldata. We need to extract this signature and then figure out what to do with it.
Solidity will create function signature hashes under the hood so you don’t have to, but Huff is a bit too primitive for that. We have to supply them directly. We can identify the ERC20 function signatures by pulling them out of remix:

We can parse a function signature by extracting the first 4 bytes of calldata and then perform a series of if-else statements over every function hash.
We can use the bit-shift instructions in Constantinople to save a bit of gas here. 0x00 calldataload will extract the first 32 bytes of calldata and push it onto the stack in a single EVM word. i.e. the 4 bytes we want are in the most significant byte positions and we need them in the least significant positions.
We can do this with 0x00 calldataload 224 shr
We can execute ‘functions’ by comparing the calldata with a function signature, and jumping to the relevant macro if there is a match. i.e:
0x00 calldataload 224 shr // function signature dup1 0xa9059cbb eq transfer jumpi dup1 0x23b872dd eq transfer_from jumpi dup1 0x70a08231 eq balance_of jumpi dup1 0xdd62ed3e eq allowance jumpi dup1 0x095ea7b3 eq approve jumpi dup1 0x18160ddd eq total_supply jumpi dup1 0x40c10f19 eq mint jumpi // If we reach this point, we've reached the fallback function. // However we don't have anything inside our fallback function! // We can just exit instead, after checking that callvalue is zero: UTILS__NOT_PAYABLE<error_location>() 0x00 0x00 return
We want the scope of this macro to be constrained to identifying where to jump — the location of these jump labels is elsewhere in the code. Again, we use template parameters to ensure that jump labels are only explicitly called inside the macros that they are defined in.
Our final macro looks like this:
template <transfer, transfer_from, balance_of, allowance, approve, total_supply, mint, error_location>
#define macro ERC20__FUNCTION_SIGNATURE = takes(0) returns(0) {
0x00 calldataload 224 shr // function signature
dup1 0xa9059cbb eq <transfer> jumpi
dup1 0x23b872dd eq <transfer_from> jumpi
dup1 0x70a08231 eq <balance_of> jumpi
dup1 0xdd62ed3e eq <allowance> jumpi
dup1 0x095ea7b3 eq <approve> jumpi
dup1 0x18160ddd eq <total_supply> jumpi
dup1 0x40c10f19 eq <mint> jumpi
UTILS__NOT_PAYABLE<error_location>()
0x00 0x00 return
}
Setting up boilerplate contract code
Finally, we have enough to write the skeletal structure of our main function — the entry-point when our smart contract is called. We represent each method with a macro, which we will need to implement.
#define macro ERC20__MAIN = takes(0) returns(0) {
ERC20__FUNCTION_SIGNATURE<
transfer,
transfer_from,
balance_of,
allowance,
approve,
total_supply,
mint,
throw_error
>()
transfer:
ERC20__TRANSFER<throw_error>()
transfer_from:
ERC20__TRANFSER_FROM<throw_error>()
balance_of:
ERC20__BALANCE_OF<throw_error>()
allowance:
ERC2O__ALLOWANCE<throw_error>()
approve:
ERC20__APPROVE<throw_error>()
total_supply:
ERC20__TOTAL_SUPPLY<throw_error>()
mint:
ERC20__MINT<throw_error>()
throw_error:
0x00 0x00 revert
}
…Tadaa. Finally we’ve set up our pre-flight macros and boilerplate code and we’re ready to start implementing methods!
But that’s enough for today. In part 2 we’ll implement the ERC20 methods as glistening Huff macros, run some benchmarks against a Solidity implementation and question whether any of this was worth the effort.
Cheers,
Zac.





