Universal SNARKs, 2019–present, and PLONK benchmarks
A refresher on Part 2— the final punchline we want to reach is the enabling of Dark Contracts — allowing confidentiality and anonymity of arbitrary blockchain transactions.
But so far, SNARKs have required a new trusted setup for each new smart contract edit (a la Groth 16).
This overhead kills Project Dark Contract dead in the water.
The Universal SNARK
Because of this seemingly intractable feature of SNARKs (a new setup for each contract alteration), Dark Contracts looked in feasible — until January 2019, when Mary Maller and Sean Bowe et al released an amazing and unexpected new species of SNARK, which they named ‘Sonic’.
This new SNARK was universal — that is, with just one setup, it could validate any conceivable circuit (up to a predefined level of complexity).
Another big step forward in the short evolution of zero knowledge systems.
Sonic is Universal, But Slow
Unfortunately though, this magical ‘universality’ did not come for free.
Making Sonic universal added ~2 orders of magnitude onto proof construction times, compared with non-universal SNARKs.
And if your laptop needs to spend 30 minutes constructing a “spend” transaction for a private token, that’s bad news — you just won’t use it, will you?
So how to make these Universal SNARKs fast?
Sonic → PLONK
Fortunately, a chance meeting between Ariel Gabizon and Zac Williamson at Binary District workshop in London helped unlock another breakthrough — a SNARK by the name of PLONK.
Zac had three principal papers in his mind when he ran into Ariel— Sonic, AuroraLight (by Ariel), and a paper by Jens Groth and Jonathan Bootle about expressing problem statements as polynomial identities.
I’ll let him regale the tale below, but first —
How do you Build a SNARK?
To make a SNARK, you need some logical and consistent way to describe logical statements (ultimately these statements will come from higher-level smart contract code).
Usually this is done through arithmetical circuits — in a not dissimilar manner to the way that all computer programs you use on a daily basis are ultimately reduced to small pieces of arithmetic on the chip.
A circuit is composed of gates and wires:
- Gates take two numbers as inputs, either add or multiply them, and then emit the result through an output wire —
- Wires carry values into and out of gates
So our SNARK will need to include the following:
- A “local” consistency check — are all your gate equations satisfied?
- A “global” consistency check — do the wires correctly join the gates together to build the circuit in question?
Zac’s Notes on building PLONK
I asked Zac for his recollections of the process:
Solving the global consistency problem for universal snarks is difficult, and Sonic was the first paper to truly crack the problem. However, it’s somewhat inefficient.
Some techniques from the a paper by Bootle and Groth can be used to efficiently solve problem 1 (local gate consistency), but then solving problem 2 (global wire consistency) becomes very hard.
AuroraLight (Ariel’s paper) provides a framework around which the Bootle paper’s techniques can be adapted to create a SNARK that solves problem 1 but not 2.
This, in a very rough and undeveloped form, was what was running through my mind when I bumped into Ariel at a workshop in May. If you encode vectors as“Lagrange-base” polynomials, instead of as Laurent polynomials, can you implement a Sonic-style permutation check? I thought the answer was “no”, and had stashed the problem away into the mental equivalent of a rusty filing cabinet in the basement behind a sign that says “beware of the leopard”.
I thought I might as well ask one of the best cryptographers in the field about it — maybe he has a trick up his sleeve. The following day at the workshop, he came up to me and said:
“Oh hey, by the way I have a solution to that problem from earlier…”
The next three months resulted in an exhilarating collaboration between AZTEC Protocol and Protocol Labs, culminating in the release of PLONK in August 2019.
So, how fast is PLONK?
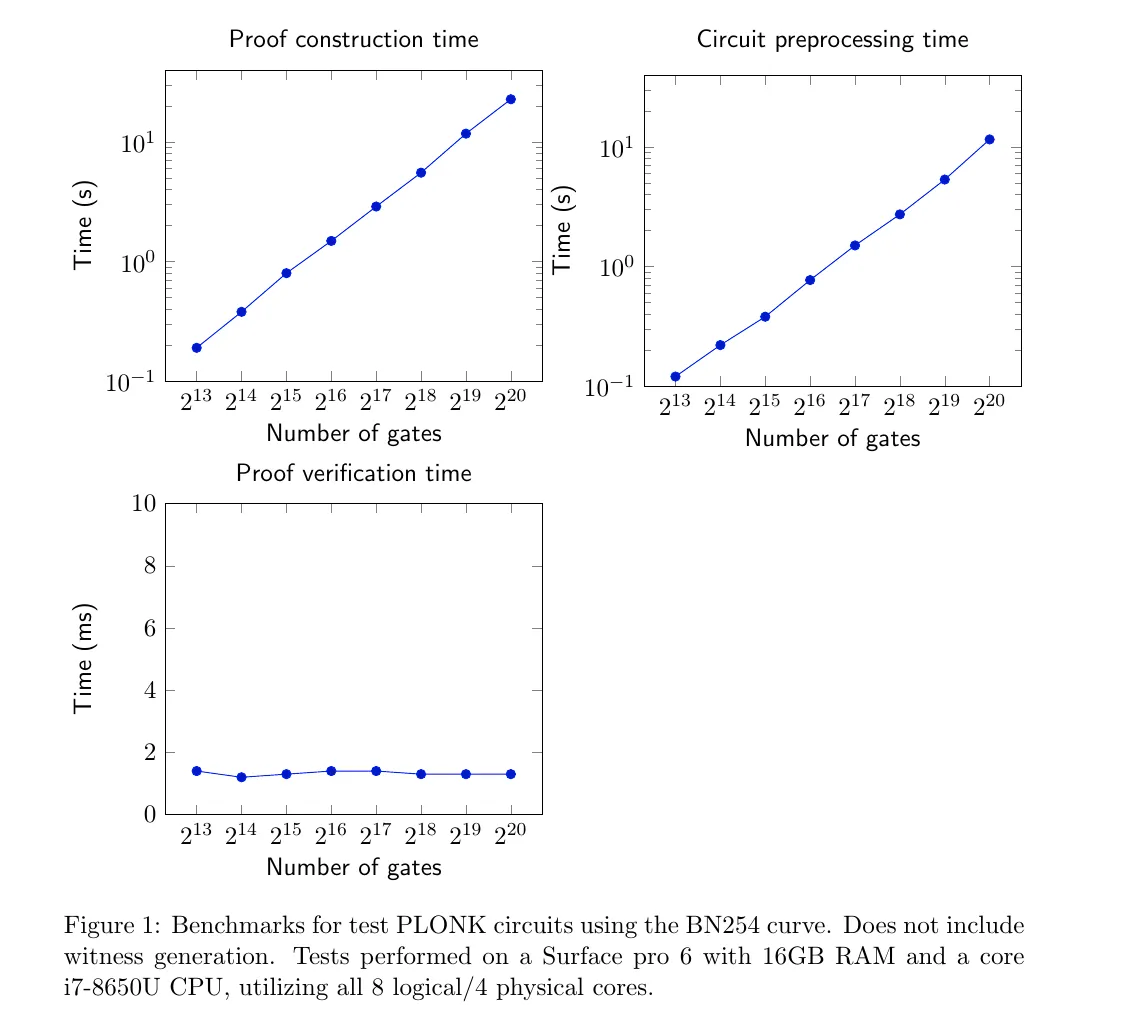
Very! Our implementation of PLONK is advanced enough to publish benchmarks for how long proof construction takes for sample circuit sizes:
PLONK is capable of chewing through a circuit with over one million gates in 23 seconds, on entirely standard hardware. No server farms or HPC clusters here — those figures came from a Microsoft Surface tablet.
To give some context, we think that a typical private transaction on Ethereum will clock in at ~128,000 to 512,000 PLONK gates. This means that PLONK can be used to programme complex logical statements in a manner that preserves perfect privacy.
To our knowledge, no other fully succinct, universal proving system comes close to these figures.
So what else is out there?
PLONK isn’t the only child of Sonic — in a summer that saw a gush of cryptographic techniques enter the fray, another fresh SNARK came into the world, created by Sonic’s original authors.
Along Came Marlin
Marlin is its name — a contemporary universal SNARK with higher efficiency than Sonic. It differs from PLONK in a couple of important ways:
- Circuit Type — Marlin validates the classical R1CS construction that has formed the foundation of SNARK proofs to date. PLONK instead uses fan-in-two gates with unlimited fan-out. Both models describe the same overall ‘universe’ of circuits, but in subtly different ways.
- The ‘global’ consistency check — PLONK uses a permutation argument to check that wire values are copied correctly along the circuit (essentially stitching wires onto other wires, an verifying they contain the same values), whilst Marlin checks that more general linear relations hold between the circuit multiplication gates. Marlin does this by the randomised sumcheck approach that has been used in papers like Aurora.
The big challenge for obtaining succinct verification via the random sumcheck route is that randomly combining the linear constraints boils down to evaluating a publicly known bi-variate polynomial, whereas polynomial commitment schemes can only efficiently handle univariate polynomials.
A key innovation of Marlin (a technique also central to the concurrent Fractal construction), is a method to verifiably evaluate such a bivariate when it is sparse (i.e. mostly vanishes) on inputs from a multiplicative subgroup.
— thanks to Ariel Gabizon of Protocol Labs for this succinct explainer.
The Benchmarks
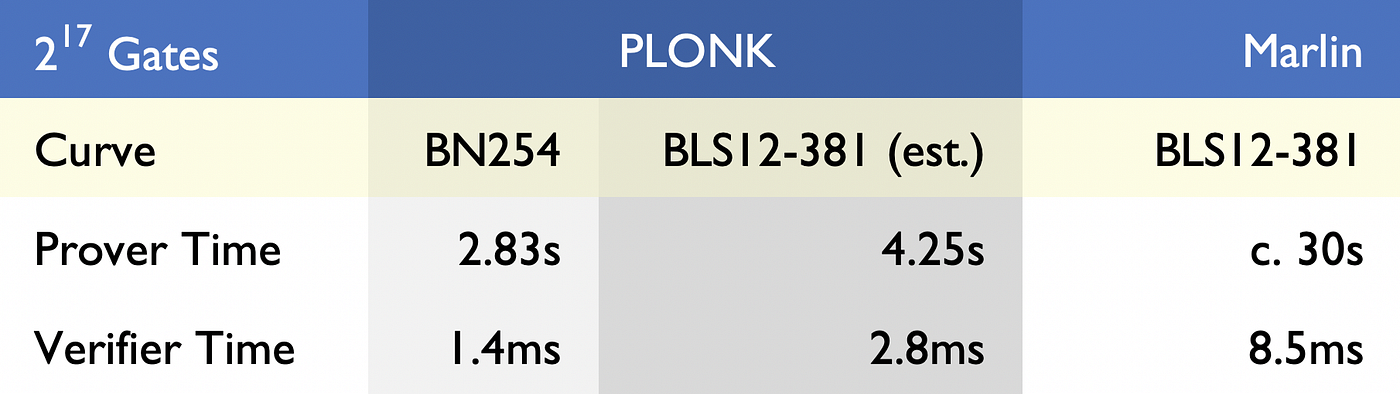
We’ve had a lot of community requests to directly compare the performance and issued benchmarks for Marin and PLONK.
Efficiency — Comparing the efficiency of different proving systems is always a bit subjective. But there is a simple heuristic we can use — proof construction times are generally dominated by the number of ‘elliptic curve scalar multiplication’ operations a prover must perform. If n is the number of addition + multiplication gates in a circuit, PLONK requires the prover perform 9n scalar multiplications. Marlin requires 21n . This does come with terms and conditions attached though — Marlin represents circuits in a very different way to PLONK, and there could be some scenarios where Marlin is more efficient than PLONK — if your circuit is composed from a lot of addition gates that have a very large fan-in (large fan-in meaning that the circuits contains gates that add lots of variables together in one go).
Before presenting them, there are some health warnings in doing so, and we urge the reader to consider carefully the effects of these assumptions:
- PLONK has been benchmarked over the BN254 curve (the only pairing-friendly curve that Ethereum smart-contracts can efficiently access), whilst Marlin has been run on the BLS12–381. On a purely like-for-like basis, we conservatively estimate that equivalent benchmarks on the BLS curve would raise PLONK’s metrics by (very roughly) 50% for the prover, and 100% for the verifier. This assumption is used to generate an estimated benchmark over BLS12–381
- PLONK was run using a highly optimised library built by AZTEC Protocol, much of which is implemented in highly efficient x64 assembly code. We also use an efficiently computable endomorphism available to short Weierstrass curves, to speed up our scalar multiplication algorithms.
Get in Touch
Whether you’d like to participate in the ceremony, apply to work at AZTEC Protocol, find out more about using our cryptosystems in your dapp, or just chat, please get in touch at hello@aztecprotocol.com or join our Telegram and Discord channels.