

This report explores the potential behind zero-knowledge proof (“ZKP”) identities (“ZKIs”) as an innovative solution for online age verification, offering the dual advantage of enabling robust identity verification while safeguarding personal information.
The global political discourse around protecting underage internet users is heating up as lawmakers struggle to achieve safe and secure internet access for minors without imposing on civil liberties.
The European Parliament’s global estimates reveal that one in three children is an internet user, and one in three internet users is under 18. As digital consumption by minors grows, policymakers worldwide are pushing for more stringent age verification laws. However, these efforts are increasingly met with legal and constitutional challenges.
This report explores the potential behind zero-knowledge proof (“ZKP”) identities (“ZKIs”) as an innovative solution for online age verification, offering the dual advantage of enabling robust identity verification while safeguarding personal information.
Click here to read the full report.
After 7 years of building in the open, last month we announced that Devnet is now live. This marked a huge milestone for Aztec and the Ethereum community by enabling private, client-side smart contract execution with robust public verifiability.
To celebrate we launched Alpha Build, a series of three developer sprints with up to US$100,000 in prizes and the opportunity to deploy on the Aztec for the first time. The first sprint, Alpha Build 1, focused on payments, wallets, programmable accounts, and fees. It garnered 50 participants, 6 teams, and a total of 13 amazing projects, ranging from wallets using Ethereum signatures to cloud based wallet features and beyond.
Starting October 8th - October 29th, 2024, the second sprint, Alpha Build 2 (AB2), will focus on identity and social. In this developer sprint, we’re seeking real-world use cases for privacy-preserving identity verification. We want to explore applications of zero-knowledge (ZK) technology, including innovative uses that integrate email verification and social attestations, as well as a modular approach to creating privacy-first applications.
Select one idea from the list below or suggest your own to the Aztec Team before beginning the challenge. Please detail your choice in your project’s ReadMe, or you can utilize an existing zkEmail circuit in Noir.
Some ideas to help get you started:
See the full list of zkEmail's project ideas for more inspiration on novel ways in which email can be used for verification.
For this challenge, we’re looking for 3 things:
Some ideas to help you get started:
The evaluation criteria for AB2 emphasize innovation in privacy preservation, assessing how effectively the proposed solution safeguards user data while maintaining practical viability, including proving times and transaction fees.
The Aztec Team will also account for potential impact on the Aztec ecosystem and how well the solution leverages its unique features, along with demonstrating tangible real-world applications and benefits.
Solutions that excel in these areas will be prioritized for their ability to drive meaningful advancements in privacy and utility within Aztec.
Don’t miss your chance to deploy on the Aztec Network for the first time and for a piece of the US$100,000 prize pool.
To get started, fill out the Alpha Build Application. We will review applications and, if selected, invite you to join a private Discord channel for Alpha Build. Join us October 3, 2024, at 11:00 a.m. ET on X to hear more about Alpha Build 2 from our President and Co-Founder, Joe Andrews as we explore challenges, themes, and innovative ideas.
Stay updated on all things Noir and Aztec by following Noir and Aztec on X, and join the Aztec developer community on Discord.
In blockchain narrative, the term “zero knowledge” entered our vocabulary when rollups first emerged. In particular, we’ve heard it a lot in the context of zero knowledge rollups (ZK-rollups). But, zero knowledge technology has existed for years before. The first article on zero knowledge was published back in 1989.
In this blog, we’ll break it down to clarify what zero knowledge (ZK) is and what it ISN’T (the latter might actually be more interesting than the former). We’ll investigate if ZK-rollups have any ZK for real, and if not, why they get to use the term at all, and dive into the difference between ZK as a technology and ZK as a marketing term.

For those who need answers right away:
*by privacy we mean (i) user privacy (transaction sender and recipient), (ii) data privacy (payload of the transaction, e.g., the asset or value being transacted), and (iii) code privacy (the program logic).
Now let’s dive a bit deeper.
If we want to discuss ZK in a rollup context, we first need to understand zero knowledge property on its own. As we mentioned above, the concept of ZK was introduced in 1989 (years before the first blockchain was baked) in a paper titled, “The knowledge complexity of interactive proof systems.” It wasn’t until around 2018 that the Ethereum community figured out ZK might be a good fit for a rollup universe.
We usually consider zero knowledge as a property of a proving system. In blockchain, we often say ZKP, meaning zero knowledge proof. But “proof” might mean proof of statement or proof of knowledge. So, in the next section of this article, we will differentiate between the two types of proofs.
Proof of statement proves that a statement is true without revealing anything about the statement itself.
Examples of statements:
Proof of knowledge proves that the person making an assertion has some knowledge about the statement.
So, if we look at the examples from the previous paragraph side-by-side:
Proof of StatementProof of Knowledgez is a square modular n: z = x^2 mod n.I know a value x such that z = x^2 (mod n).The graphs G and H are non-isomorphic.I know the isomorphism between two graphs, G and H.The number 638634389........3427 has 3 prime factors.I know the factors of the number 638634389........3427.
One should note that every proof of knowledge is a proof of statement (but not the opposite). For instance, if one proves that they know a value x such that z = x^2 (mod n), this will be proof of knowledge, but it also automatically proves that z is a square modulo n (proof of statement).
Let’s explore one of these examples to see how proof of statement and proof of knowledge can be constructed!
Let’s use the graph-isomorphism problem. To do this, we’ll say proof of graph non-isomorphism will be proof of statement, while a proof of graph isomorphism will be proof of knowledge.
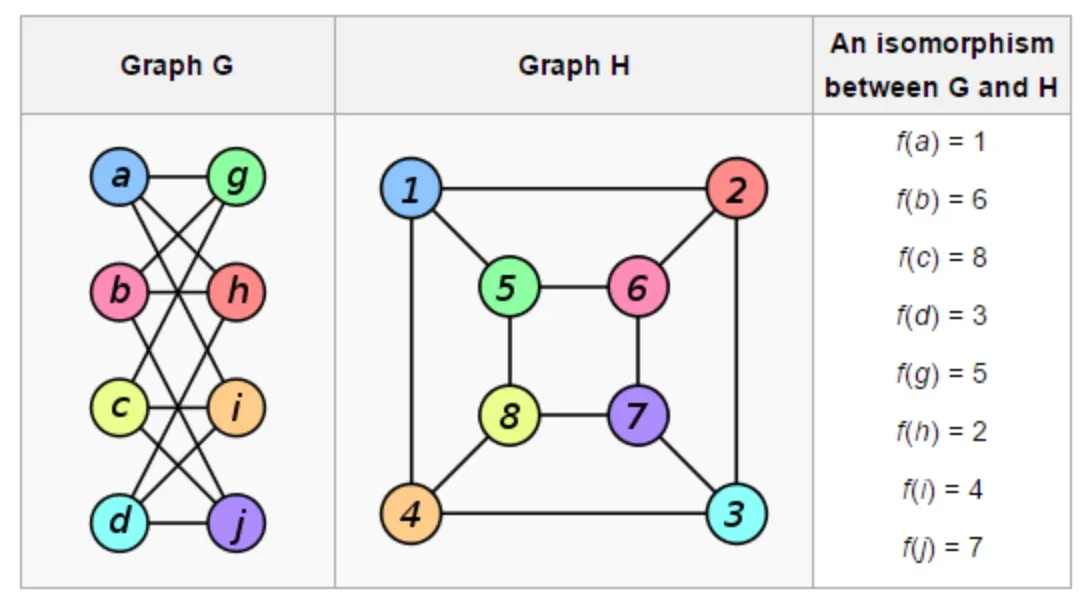
Basically graph isomorphism (denoted by ≅) is the following: two graphs with labeled nodes are isomorphic if they are "the same" up to a permutation of the labels. That is to say, there exists a permutation of the labels of one graph that results in the other graph.
More formally, we say that two graphs G and H are isomorphic if there is a bijective function f between the vertices’ labels of G and H such that there is an edge between the vertices u and v in G if and only if there is an edge between the vertices f(u) and f(v) in H.
An example of two isomorphic graphs:
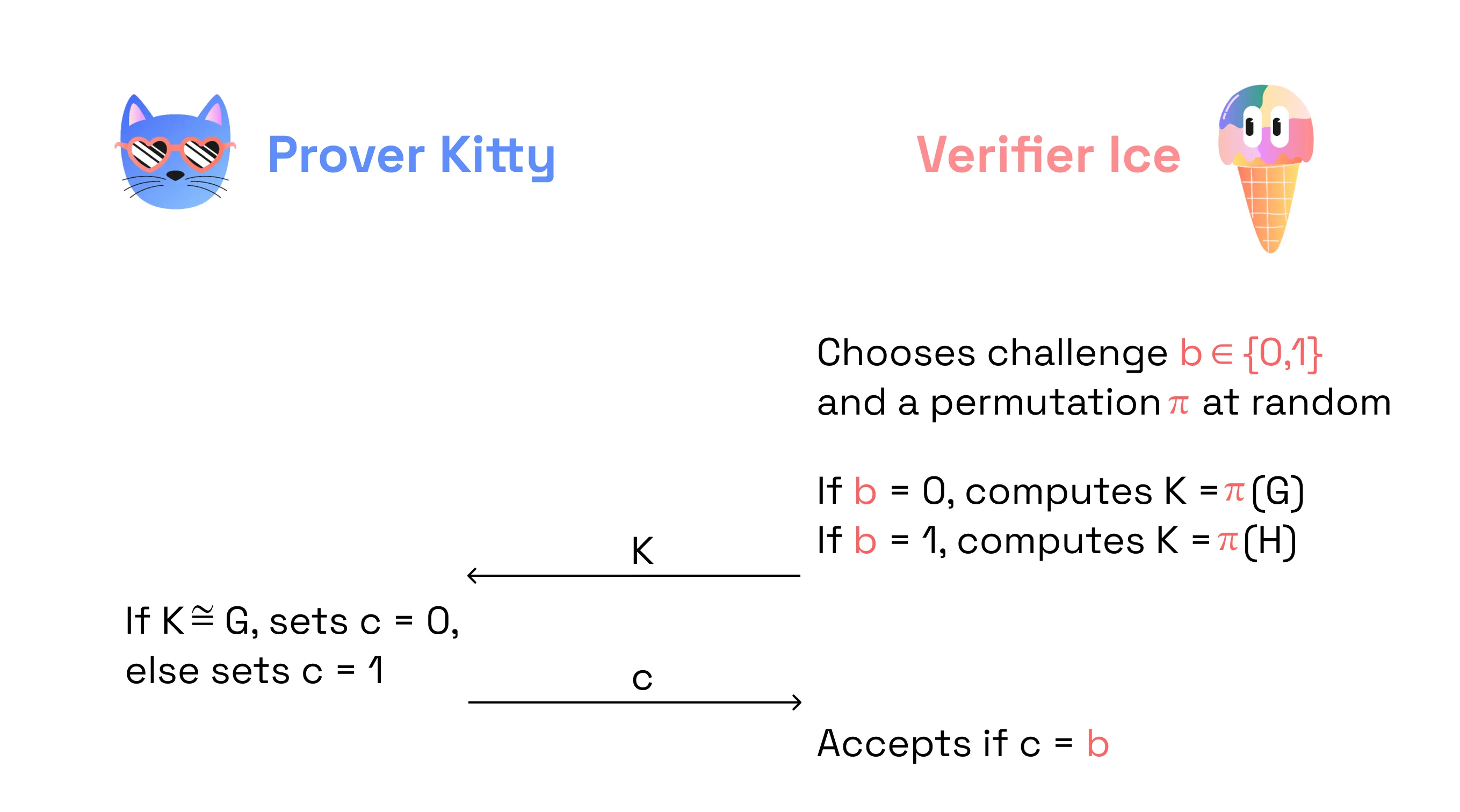
If there exists no such permutation, we say that the two graphs are non-isomorphic. Now, assume we want to prove that two graphs are non-isomorphic. We only want to prove this single fact; nothing about the graphs themselves, no other knowledge except for the statement that they are non-isomorphic.
Proof intuition:
One round of protocol:
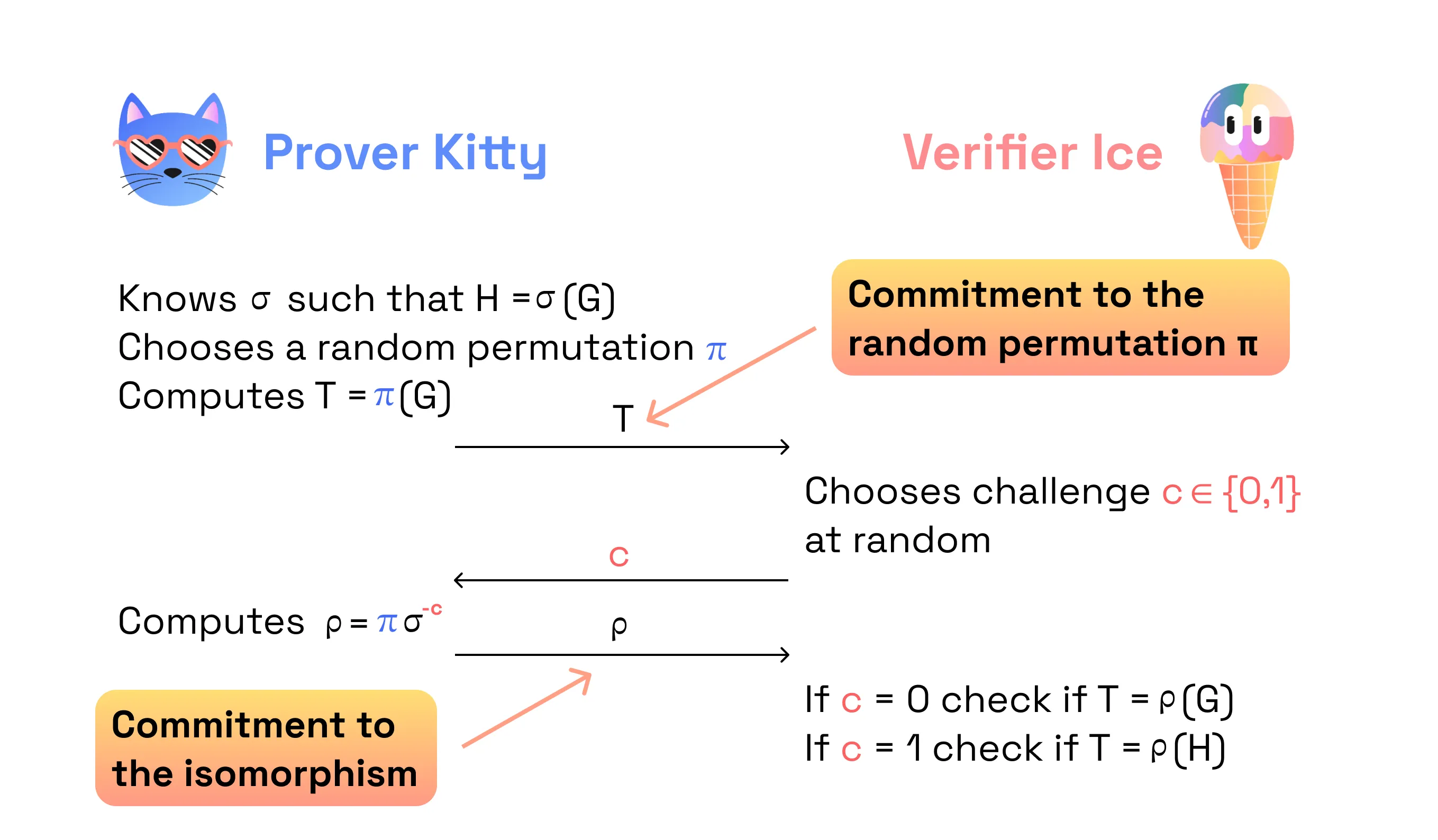
Now, let’s think… What if we want to prove two graphs are isomorphic? In other words, the Prover wants to prove that they know the isomorphism σ such that H = σ(G).
Proof intuition:
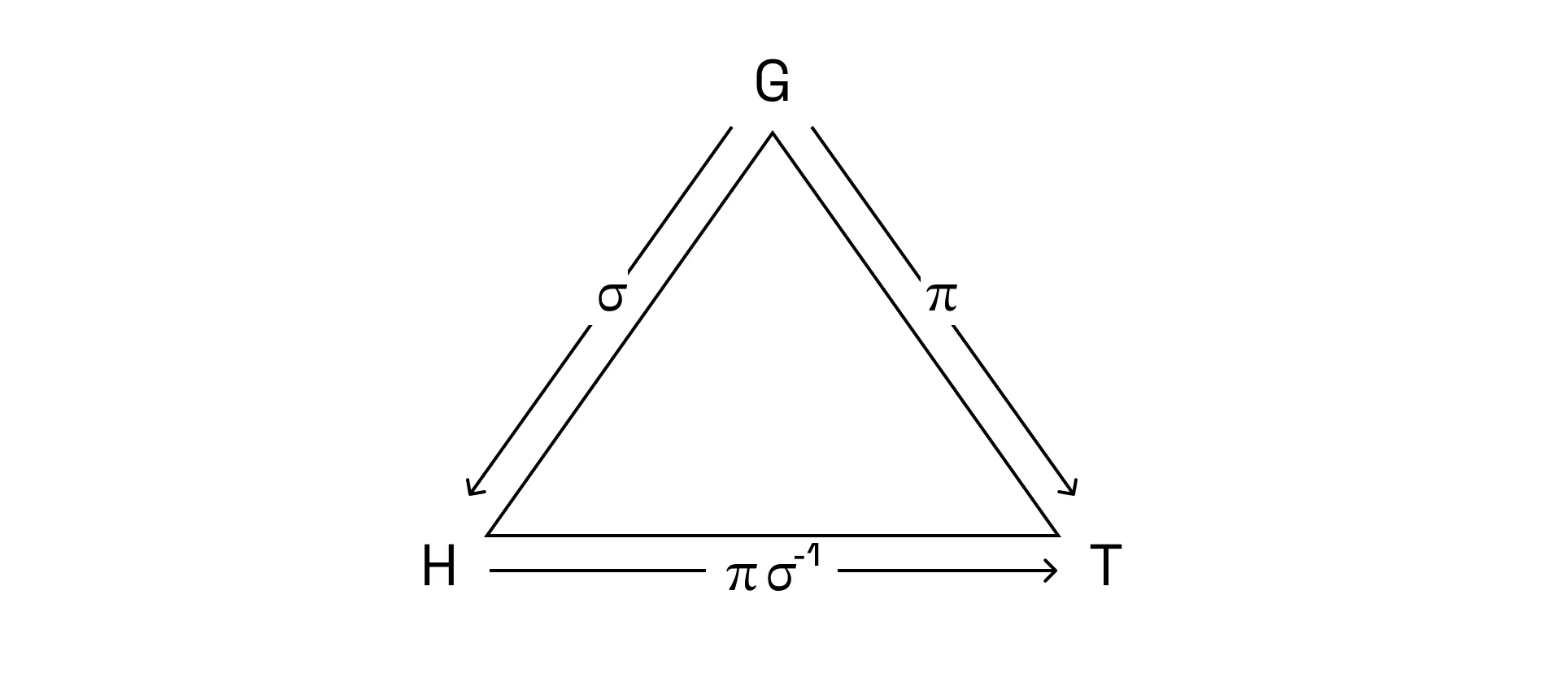
One round of protocol:
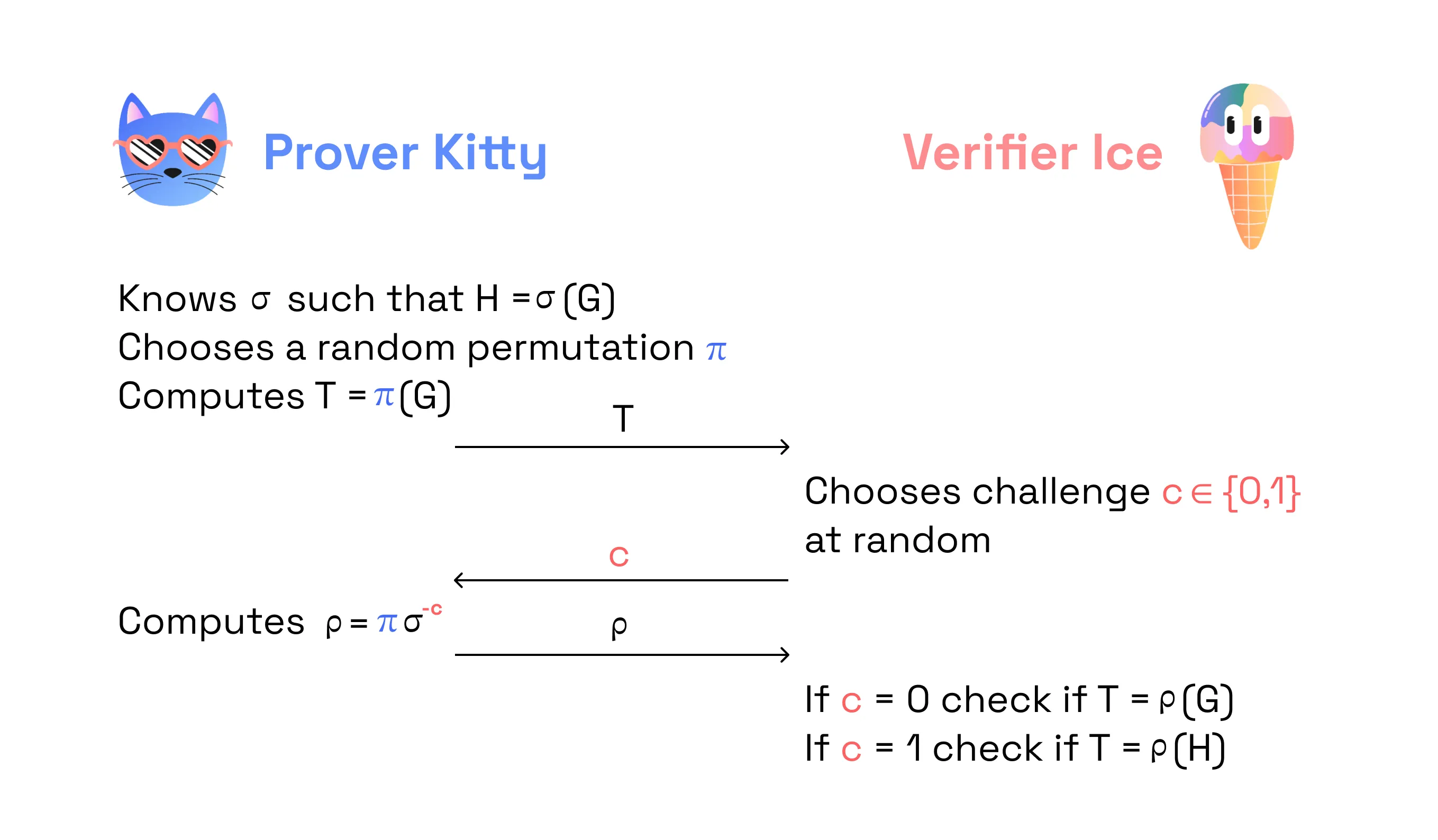
Now that we’ve explored examples of proof of statement and proof of knowledge, let’s discuss whether or not they have zero knowledge property.
Informally, zero knowledge means that a Verifier can’t retrieve any additional information from a Prover (except for the information clear from the proof itself).
In the example of graph isomorphism, proof of knowledge is zero knowledge (with honest Verifier). According to the protocol, the Prover doesn’t reveal any information on the isomorphism or permutation to the Verifier. Instead, they send the Verifier commitments and that’s it.
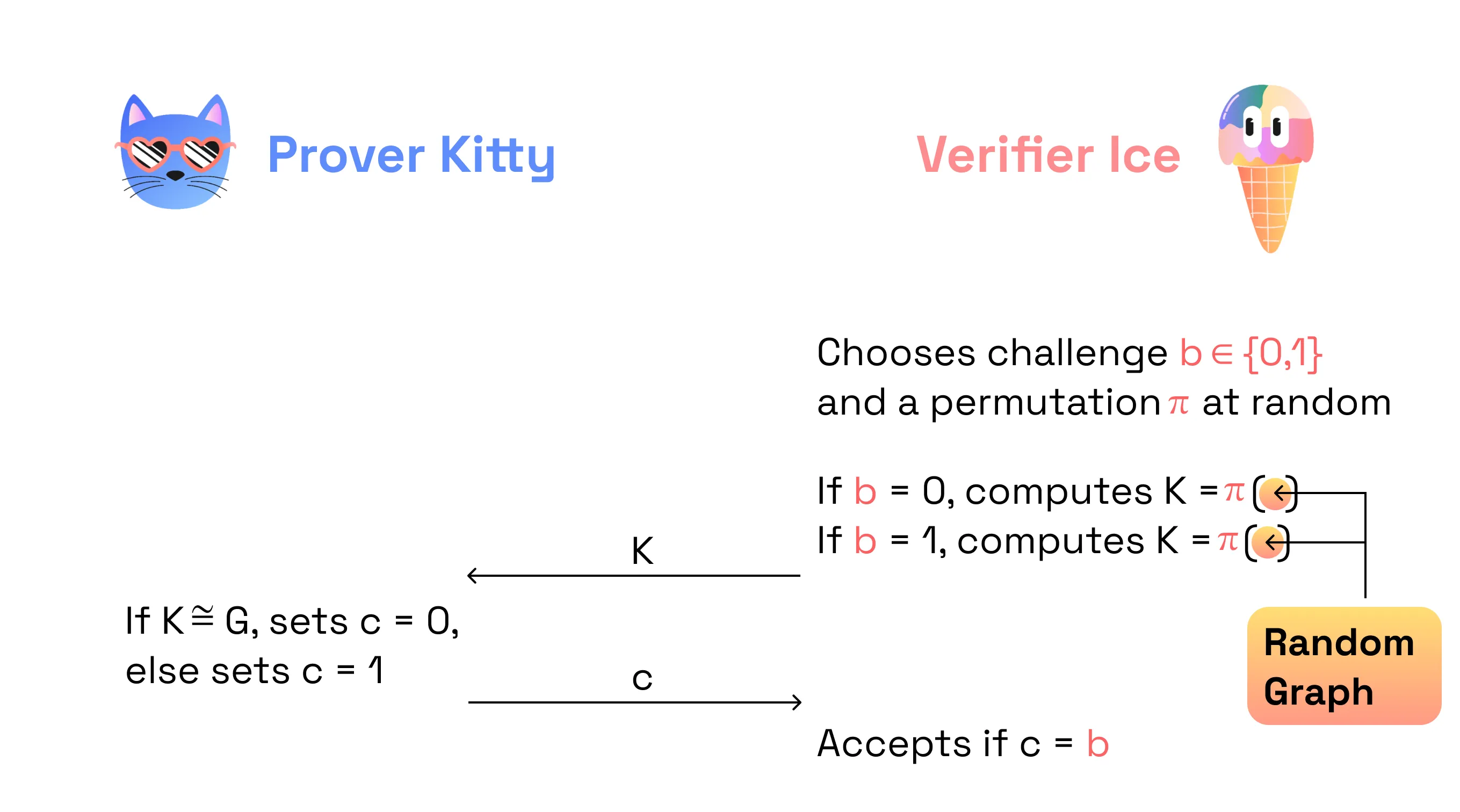
However, in the example of the proof of graph non-isomorphism, it’s not zero knowledge. Because, instead of setting K = π(G) or K = π(H), a malicious Verifier (i.e. a Verifier which deviates from the protocol) can set K = π{RANDOM GRAPH} and as a result of the protocol execution by the Prover, the Verifier will know if RANDOM_GRAPH is isomorphic to either G or H. So the Verifier is definitely able to retrieve additional information.
Can we convert our proof of graph non-isomorphism into zero knowledge? Yes, we can. The Verifier should also provide proof that (i) the graph it sends is isomorphic either to G or to H (meaning the graph they’re sending is not arbitrary), and (ii) they know the isomorphism.

One should note that most protocols in the space are only honest-verifier ZK (i.e. ZK property doesn’t hold with malicious verifier). However, this isn’t an issue because the protocols are made non-interactive with the Fiat-Shamir heuristic. Hence – there is no distinction for non-interactive protocols as the verifier cannot "misbehave.”
Now, when we differentiated between proof of statement and proof of knowledge and saw that both of them can have zero knowledge property or not have it, let’s take a look at ZK-rollup and figure out (i) does it use proof of statement or proof of knowledge, (ii) does it have zero knowledge property?

In a ZK-rollups, the logic is pretty similar to the graph-non-isomorphism problem (where we prove the statement that two graphs are non-isomorphic). In ZK-rollup, we prove the statement that the state transition was done correctly.
In this section, we’ll briefly cover how ZK-rollups work and how they utilize proofs. By “ZK-rollups,'' we mean regular (i.e. NON-privacy-preserving) ZK-rollups such as Scroll, Starknet, zksync, Taiko, and many more.
The main use of “vanilla” ZK-rollups is to enable scalability by posting a single proof of the validity of transactions.
ZK-rollups execute transactions off-chain and post proof on L1 (Ethereum) that whatever they did off-chain was done correctly. Their purpose is to prove that the new chain state is correct.
To generate a proof of correct state transition, one needs to prove that all transactions were executed correctly on given inputs.

For the sake of this, the Prover needs to know previous state and input values.
However, for the Verifier to verify the proof, they need to have the proof as well as to know new state, previous state, and input values:

There are two types of inputs, public and private. In ZK-rollups, “private input” does NOT mean “secret” even though they are called “private.” Instead, it means that private inputs are consumed by Prover only while public inputs are consumed both by Prover and Verifier (sometimes private inputs are also called “witness” as a reference to the NP complexity class). Public inputs are expensive as they need to be submitted to L1 hence we want it to be as small (“succinct”) as possible. In terms of what these inputs consist of in the context of the proof:
Public inputs (consumed by Prover AND Verifier) – all data that needs to be submitted to L1 so that everyone can update their records of the current state. This will include new state root as well as might include signatures, sender, receiver, functions, contract addresses, function arguments, newly-deployed contract data, storage slots which have changed and their new values, events that were emitted. One should note that this reveals A LOT of information to a public observer. The specific list of public inputs will depend on the specific ZK-rollup design.
Private inputs (consumed by Prover ONLY) – all information that was needed by rollup circuits to prove correctness of the state transition. This will include Merkle membership proofs (hash paths) as well as the execution trace (might include transaction inputs such as newly-deployed contract data, storage slots which have changed and their new values, and events that were emitted).
As you can see from the logic above, private inputs have nothing to do with privacy. So if a ZK-rollup is generating a proof that Alice sent Bob 1ETH, both the Prover and the Verifier will be aware of this information (i.e. no privacy at all!).
To sum it up, in the case of a ZK-rollup, we want to prove the validity of transactions, it is a proof of statement and it does NOT have zero-knowledge property because all the information (i.e. state, functions, inputs) is public and everything that is not provided explicitly can be derived by a Verifier.

That is to say, there is no ZK in a vanilla ZK-rollup. Why is it called ZK-rollup then?
.webp)
Maybe… For the sake of marketing =)
Short answer: yes, it can. While the main use of “vanilla” ZK-rollups is to enable scalability, the main use of Aztec is to enable scalability AND allow privacy. And, it utilizes ZK exactly for the privacy purpose.
Aztec provides privacy by means of client-side proof generation, i.e. whatever should be processed privately is processed on the user’s device and then a proof of its correct execution is supplied to the mempool.
Processed privately means that
Client-side proofs are then verified by the sequencer (who manages the mempool).
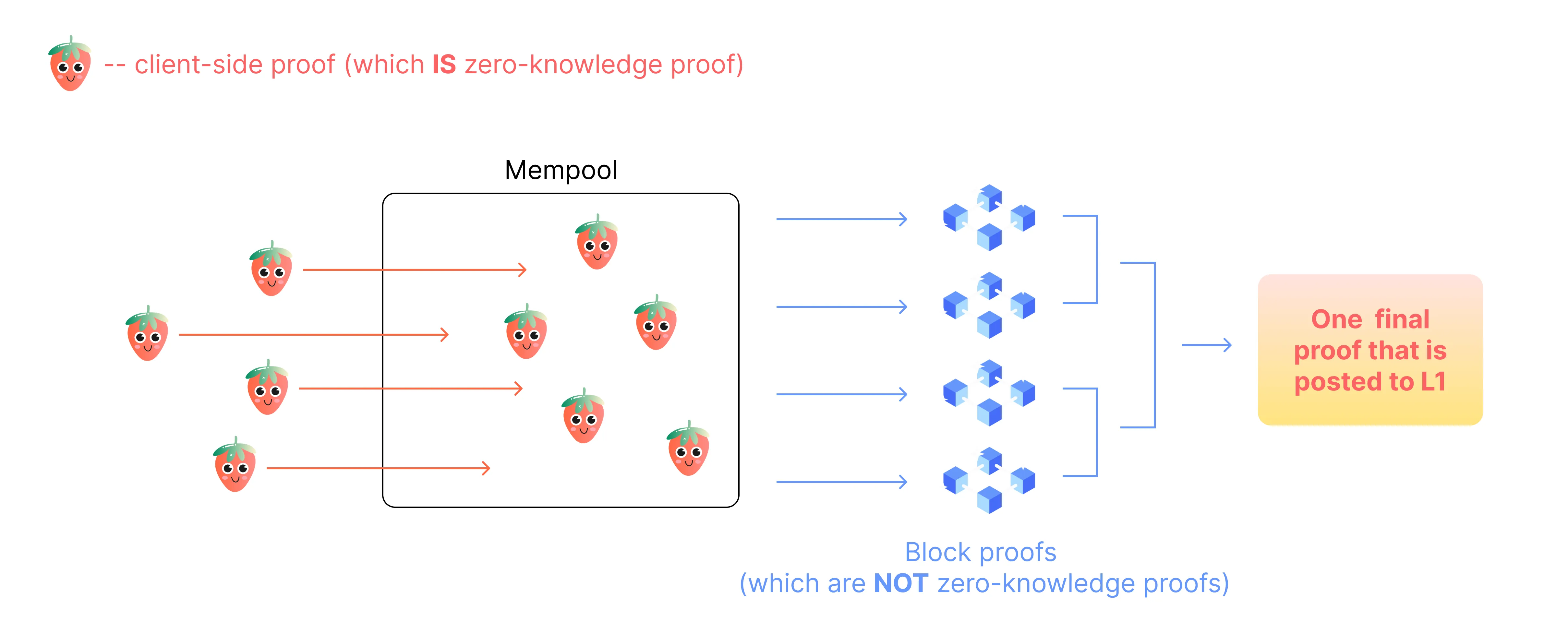
In this case, client-side proof is a zero knowledge proof of statement: the sequencer verifies the proof validity without any information about what was executed on the client-side, and is unable to retrieve any information about it.
After client-side proofs have been verified by the sequencer, everything is similar to a vanilla ZK-rollup mechanism as described in the previous section. That is to say, Aztec ZK-rollup first generates a number of client-side proofs (which are zero knowledge proofs) and then a block proof (which is not zero knowledge).

It’s not possible to add privacy ad-hoc to an already existing ZK-rollup. It should be designed to be private from the very beginning.
One first needs to give a precise definition of “privacy” as the statements proved, depending on the rollup design, may reveal unnecessary information and harm user privacy.
If builders want their dApps to interact with the external world; meaning that dApps aren’t monolithically private but instead allow some functions and variables to be private while some functions and variables stay public (e.g. necessary for AMMs, lending protocols, etc.), rollup state management becomes very non-trivial. Now it has to process public and private state updates separately. However, it’s exactly the latter approach that unlocks dozens of use cases we’ve been dreaming about for years! (Think programmable on-chain identity management and DeFi alternatives to conservative financial institutions).
As of today, Aztec is one of very few privacy-preserving L2s on Ethereum where privacy is provided by processing private information on the client-side. Check out this article to dive into client-side proof generation and this article to learn more about Aztec smart contracts anatomy allowing for hybrid private and public state management.
Ready to join Aztec’s building pioneers? Let us know by filling out this form.
Many thanks to Palla, Patrick, and Brecht for review.
We’ve all heard that “privacy UX sucks.” We tend to agree.
Users want to drive a car, not change the oil. We previously discussed how we abstract Aztec’s underlying UTXO architecture with Noir Lang and Aztec.nr, Aztec’s smart contract framework.
Today we’ll cover how we improve transaction processing via account abstraction and composable public-private design.
To date, protocols focusing on user privacy have exposed the underlying privacy architecture. And it turns out that users don’t like dealing with the nuts and bolts inside the machine.
We think user-friendly abstractions represent the future of intuitive UX in blockchains–a necessary step to bringing crypto to parity with web2. We’ll define transaction paths, explain what they mean, and explore how they future-proof the Aztec experience for developers and users.
In Ethereum, every account is controlled by a private key, commonly derived from a mnemonic. If you’ve ever created an Ethereum wallet, you’ve seen the list of words you need to engrave, memorize, or at minimum jot down to secure your account.
Note that we’re talking about Ethereum externally-owned accounts here (EOA’s), not contract accounts, since on Ethereum, EOA’s are the only accounts that can initiate transactions.
When you initiate a transaction on Ethereum, the network expects a signature from the private key that controls the account. If you create a signature that matches the public key associated with the transaction, the transaction is submitted with a transaction payload that instructs the Ethereum Virtual Machine on exactly what functions to execute.
At Aztec Labs we’ve been thinking hard about forms of account authentication beyond signatures. The use of seed phrases has significant issues:
📕 Read this post by Santiago Palladino for more about the account abstraction designs being developed for Aztec on our Discourse forum
So how do we get around seed phrases and private keys as the sole forms of account validation? Seed phrases are just one very secure but very flawed form of account validation. There are myriad methods of account validation, spanning the spectrum from very secure to totally insecure, from intuitive to confusing, including but not limited to:
Keep in mind account validation can be as secure as you want it to be. One simple account validation scheme would be: “If you click the ‘yes’ button the account is validated.” It wouldn’t be secure AT ALL, but you could do it!
Account abstraction is confusing as a term, since it encompasses “everything but seed phrases,” but the holy grail of authentication would include three factors:
Aztec allows for combining all three.
But Aztec’s improvements to Ethereum go beyond the implementation of alternate authentication schemes.
Aztec’s transaction anatomy is also a bit different — users send proofs of computation rather than signing transactions from an EOA.
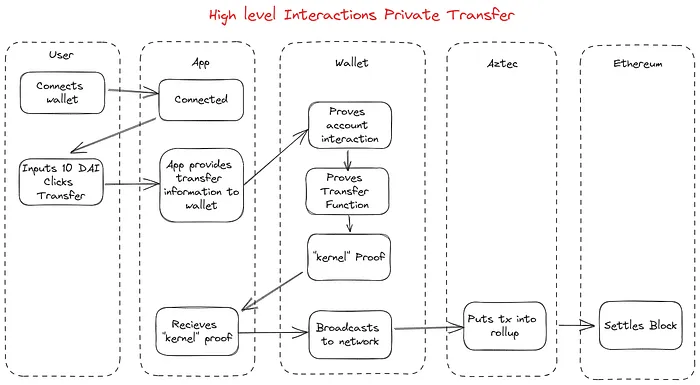
Here is the flow diagram for an Aztec transaction:
We’ll talk through each in turn.
Before we carve the patient open and look at its guts, know that there are two transaction paths within Aztec: private transactions and public transactions, each with their own attributes.
At the center of these transactions is something called the kernel circuit. The kernel circuit is the beating heart of the Aztec system, and validates private transactions. We’ll get back to it in a second.
For now let’s talk about what a blockchain transaction in general is:
We already discussed how Aztec allows for new forms of authorization, but how does it process transactions?
Aztec is a completely new execution environment beyond the EVM, and uses client-based zero knowledge proofs to prove individual transactions. That means the application developer’s job is to constrain functions appropriately and prove user intent.
Application developers can constrain user intents by writing smart contracts using Aztec.nr. In the private transfer example, the circuits behind the smart contract are checking a few conditions:
The nullifier, new note, an encrypted log are all made public, but kept encrypted, such that the public information tells you nothing about what happened. Roughly all an observer can see is “a transaction happened here but I’m not sure what.”
That’s the core of Aztec’s value proposition — we know with mathematical certainty transactions are happening that follow blockchain rules, but we can’t derive any information about those transactions.
📕 See our previous piece on how Aztec’s privacy abstraction works
The path for public transactions is slightly different, as Aztec relies on the familiar Ethereum account-based model for public transactions.
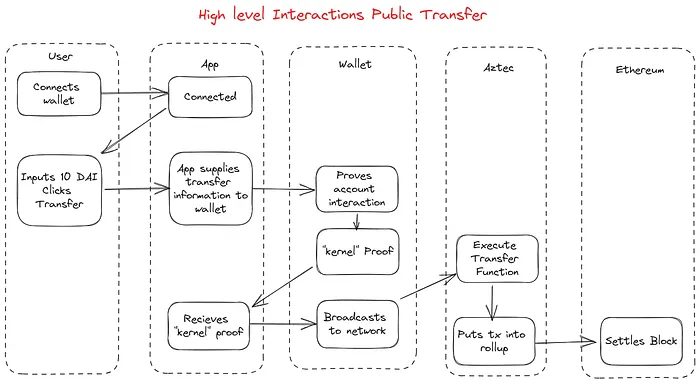
The key to Aztec’s public transactions are unconstrained functions–Aztec’s public VM bytecode. Unconstrained functions just do “normal code stuff.” And by “normal code stuff” we mean simply execution code rather than proving execution as in Aztec’s private execution path. Unconstrained functions don’t lay down constraints. They just executes code.
If Aztec is a world computer, then unconstrained functions are the instructions the computer understands. Just like the EVM executes Solidity, the Aztec VM executes Aztec bytecode.
One key difference between the private and public execution paths is when code gets executed. In the private transaction example, code must be executed and proven locally–that is, before proof of the transaction is sent to Aztec’s network of nodes.
In the public execution path, the wallet has to receive authorization, but doesn’t process the transaction, instead sending transaction details onward to an Aztec node which then creates a proof of execution and inserts the proof into a block.
Because privacy is no longer a concern with public transactions, they can be sent unencrypted to the node to do efficient batch processing, rather than relying on a user’s local device.
Privacy UX sucks. Zero knowledge is complicated. Our goal is two-fold:
Great privacy-first applications will be built on the backs of best-in-class tooling that makes it easy to build powerful software that makes preserving privacy smooth and intuitive for users.
That means more code, less cryptography.
To learn more about Aztec generally, keep up to date on our Discourse, where we discuss major protocol decisions like upgrade mechanisms and decentralizing sequencers.
For more technical news on Aztec and Noir, join our e-mail newsletter:
Aztec Labs is on the lookout for talented engineers, cryptographers, and business people to accelerate our vision of encrypted Ethereum.
👪 If joining our mission to bring scalable privacy to Ethereum excites you, check out our open roles.
And continue the conversation with us on Twitter.
Thank you to Bruno Lulinsky and Maddiaa for input on this piece.