At Aztec we’re excited to have launched zk.money this week, enabling efficient, completely private transactions on the Ethereum blockchain.
JavaScript is not available.
So, it seems you noticed … Yes, Private Layer 2 ZK-Rollup has arrived on Ethereum | https://t.co/p2DxzB4sm9
This is something we’ve building towards for almost 3 years now.
The privacy our users enjoy does not rely on trusted third parties or additional consensus algorithms. The security of our system is backed up by ironclad zero-knowledge cryptography, with the consensus of our network being derived directly from the strengh of Ethereum’s consensus protocol via our zero-knowledge proof verification smart contracts.
This is the first time a privacy-preserving rollup has been deployed to Ethereum, or any other public blockchain for that matter.
Getting to this point has been quite the adventure for us. When you trigger a private send from zk.money, your computer will grind through some of the most advanced number theoretic computations ever pushed through a web browser.
We’ve had to design a lot of new tech to pull this idea into the world. From inventing the cryptographic protocol we use and building an optimized proving system, to the backend server that aggregates and processes zero-knowledge transaction. This article is a dive into the tech behind our private ZK-rollup and its inner workings.
What is a private ZK-rollup?
Zero-Knowledge-rollups are a way of scaling Ethereum. Instead of having the blockchain processing every transaction in a block, the block’s transaction inputs and outputs are sent to Ethereum, along with a zero-knowledge proof that the transaction outputs have been correctly computed from the inputs. This reduces the computational burden on the network and reduces the amount of smart contract storage data that must be modified.
Traditional ZK-rollups aren’t privacy preserving despite their name; the ‘zero-knowledge’ refers to using ZK-Snarks for scaling only.
Private ZK-rollups are a different beast. As well as providing the scaling benefits, the transaction inputs/outputs are encrypted. The zero-knowledge proof that proves the correctness of every transaction also proves that the encrypted data was correctly derived from the non-encrypted ‘plaintext’ data. But the plaintext is known only to the users that constructed their private transactions.
The rollup cannot simply process a list of transactions like before, it must verify a list of zero-knowledge proofs that each validate a private transaction. (This extra layer of zero-knowledge proof verification is why they’re called ‘ZK-ZK-rollups’).
The result is reduced-cost transactions with full transaction privacy, even from the entity making the rollup! Both the identities of senders/recipients are hidden, as well as the values being transferred.
Despite this, users of the protocol can have complete confidence in the correctness of transactions (no double spending etc), because only legitimate transactions can produce a valid zero-knowledge proof of correctness.
Plonk: the world’s fastest universal ZK-SNARK
In theory ZK-ZK-rollups have been known about for several years, but nobody has managed to deploy one in practice, until now. There were an immense number of technical hurdles we had to overcome to get to this point, not least of all having to design our own ZK-SNARK protocol to get the job done!
Plonk is our state-of-the art ZK-SNARK, developed in-house by our chief scientist Ariel Gabizon and CTO Zac Williamson. Its fast proving times, expressive method of circuit arithmetisation and lack of circuit-specific trusted setups makes it ideal for blockchains. The Electric Coin Company, Mina Protocol, Matter Labs, Dusk Network and more are all using Plonk in their latest projects.
Aztec’s ZK-ZK-rollup architecture
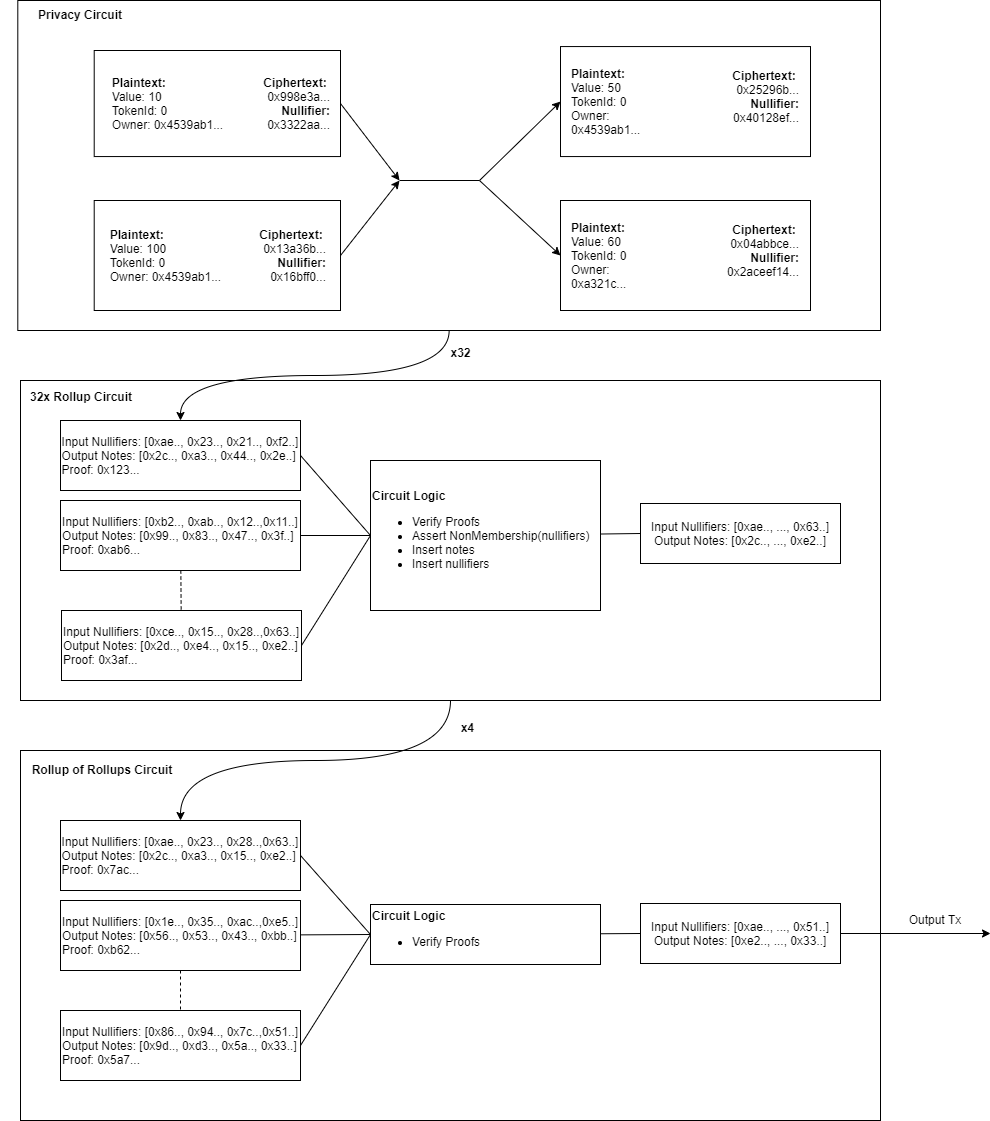
Our architecture is composed of two programs that we have encoded into ZK-SNARK ‘circuits’: A privacy circuit and a rollup circuit.
The privacy circuit proves the correctness of a single private transaction. It is constructed by users that want to send private transactions, directly on their hardware to ensure no secrets are leaked.
The rollup circuit validates the correctness of a batch of privacy proofs (currently 128) and updates the rollup’s database with the new encrypted transaction data.
The rollup proofs are constructed by a rollup provider, a 3rd party that has access to significant computing resources (for the moment, Aztec are the rollup provider. Longer term we plan to decentralize the rollup service). The rollup provider is completely untrusted. They do not have access to any user data and only see the encrypted outputs of privacy proofs. This also makes it impossible to launch selective censorship attacks, because all transactions look like uniform random numbers.
Building a ZK-ZK-rollup
Both the privacy circuit and the rollup circuit have two major challenges associated with them:
1. The privacy proof must be computed by the user, it cannot be delegated to a 3rd party.
2. The rollup circuit must efficiently verify the correctness of hundreds of privacy proofs.
The former is challenging because users are likely to interact with our software in a web browser. Executing cryptography code in a web browser is approximately 8x slower than running native compiled code, due to the WebAssembly specification lacking an opcode for full-width 64×64-to-128-bit multiplication.
The rollup circuit requires recursion, the ability to verify ZK-SNARK proofs inside ZK-SNARK circuits. Until recently, the consensus was that this required cryptographic primitives that are not supported by the Ethereum specification!
Both problems boil down to the fact that constructing ZK-SNARK proofs are slow. Basic arithmetic operations in a circuit must be converted into tens of thousands of 256-bit big-integer multiplications.
Previously existing ZK-SNARKs simply were not efficient enough to serve our needs and/or had unacceptable security trade-offs (like requiring trusted setup ceremonies for every circuit).
We put together Plonk to solve these problems. Plonk was the world’s first practical, fully succinct universal ZK-SNARK. Its ‘universal’ because only one trusted setup is required for every Plonk circuit (we completed our trusted setup ceremony, ignition, in 2020).
We have not been idle since then, and our software uses a much-improved version of our protocol, TurboPlonk.
Turbocharging Plonk
TurboPlonk is a dramatically enhanced version of our original Plonk protocol.
Existing SNARK systems can only perform basic arithmetic operations: adding and multiplying prime field elements together.
This is a bit like having to work with a computer whose ALU only has `ADD` and `MUL` instructions! This is one of the reasons why SNARK proofs are so slow to construct — transforming a program into a circuit blows up the instruction count.
Put in context, existing SNARK arithmetic is about as complex as the kind of math you could program on a 1961 Programma 101.

This restriction is because of the way the arithmetisation of traditional SNARKs is constructed. Elliptic curves are homomorphically additive ([A] + [B] = [A + B]). General homomorphic multiplication is not possible, but the bilinear-pairing enables a single homomorphic multiplication by the one way mapping into the target group.
Most ZK-SNARKs have arithmetic that directly maps to the available operations on an elliptic curve. This is codified into the Rank One Constraint System abstraction (R1CS), a method of defining circuits by creating ‘constraints’ composed of many additions, combined with a single multiplication. The current fastest R1CS-based proving system is the non-universal Groth16, currently used by Zcash.
Plonk and TurboPlonk are different. Their use of polynomial commitment schemes divorces their arithmetic from the limitations of elliptic curve group operations. i.e., we can multiply more than once per ‘constraint’.
In TurboPlonk, we use this flexibility to implement what we’re calling ‘custom gates’. Instead of just ADD and MUL gates, we have added gates that can do the following:
* 2-bits of an XOR op
* 2-bits of an AND op
* 8-bit range checks
* 2-bits of a Pedersen hash function
Still primitive by traditional standards, but at least the addition of logic operations moves us out of programmable calculator territory.
Efficient range checks, Pedersen hashes and logic operations are the bread and butter of the type of cryptography required in modern ZK-SNARK circuits. They make TurboPlonk not just competitive with non-universal proving systems like Groth16, but in many cases significantly faster.
Building the rollup proof and achieving recursion
Verifying a SNARK proof inside another SNARK circuit is traditionally a profoundly difficult task. SNARK circuits can only perform operations modulo a specific prime number p, a number defined by the elliptic curve you are using.
Verifying a SNARK proof requires elliptic curve arithmetic modulo a different prime number q. If you are using a single elliptic curve, qmust be different to pfor the curve to be secure!
How does one perform arithmetic modulo qwhen all your calculations are mod p? The ‘brute force’ approach requires emulating binary arithmetic using your ‘mod p’ arithmetic. Literally proving that individual wires in your circuit are 0 or 1, and assembling larger integers out of your bits.
You can then emulate your ‘mod q’ arithmetic using your emulated binary arithmetic.
This comes at a huge cost, the resulting system requires a revolting number of range checks, millions of them in fact.
This is the reason why recursion has proven to be a brick wall that blocks the deployment of advanced zk circuits on Ethereum. Existing solutions to the problem (e.g. Halo) utilize elegant number-theoretic constructions to get around this wall, but they require cryptographic operations that are not available within Ethereum smart contracts.
Fortunately, we designed TurboPlonk to be extremely good at efficient range checks (16x better than regular Plonk), to the point that we can sledgehammer our way through the problem and use the emulated field arithmetic approach.
We published our recursive construction in April last year. It is the only practical method of achieving recursive ZK-SNARKs on Ethereum to-date.
Achieving full privacy
Achieving full privacy in a rollup presents some unique challenges, other than the recursive SNARK problem.
We need to ensure that when a user spends a note, the spend transaction cannot be linked to any existing note.
This is achieved by using a set of ‘nullifiers’. Each nullifier represents a spent note. The encryption algorithm used to create nullifiers is different to note encryptions. This prevents linkability between notes and nullifiers.
Nullifier sets are problematic, however. To prove a note has **not** yet been spent, one needs to serve a *proof of non-membership*. To ensure our non-membership proofs have 128-bits of security, we need our nullifier Merkle tree to have a depth of 256!
Traditionally this would make membership and non-membership proofs of the nullifier set inordinately expensive. However, because of our custom Pedersen hash gate, our Pedersen hashes are 5x more efficient than systems that use R1CS and 18x more efficient than regular Plonk.
The result is that we can support depth-256 nullifier sets within our rollup architecture, which is not something that has been achieved to date.
Moreover, we are able to do this with a traditional well studied hash function. The collision-resistant properties of Pedersen hashes are well understood and we use Blake2s hashes whenever we need to model the hash function as a random oracle. We chose not use more recent SNARK-friendly hash functions due to the relative lack of cryptanalysis that has been performed on them, compared to the alternatives.
Building privacy proofs in a web browser
To give some scale to the problem, Zcash proofs can be generated in ~3 seconds on modern hardware. Universal SNARKs traditionally are about 10x slower than the Groth16 system currently used by Zcash. On top of that, we are using WebAssembly which is 8x slower than native code. That’s also assuming you can get multithreading working in the browser without browser support for WebAssembly threads (disabled after Spectre/Meltdown). Under these assumptions even a basic private transaction proof would take around 4 minutes to construct. Ouch!
But it gets worse! Our privacy circuit is larger than the Zcash circuits. We felt it was important to support social recovery of lost accounts, which requires an account management subcircuit within our privacy circuit. If we encoded our circuit in the traditional R1CS form, it would have approximately 260,000 constraints and would take up to *8 minutes* to prove in a browser.
Fortunately, TurboPlonk is up to the challenge. Our ability to efficiently evaluate hashes and bitwise logic operations crushes down the constraint count of our circuits to a more reasonable 65,535. We combined this with prover algorithms that are optimized for WebAssembly and a javascript SDK that implements a multithreaded variant of our WebAssembly prover using web workers.
On top of that, we have put together a new elliptic curve multi-scalar multipliation algorithm. It was, to our knowledge, the first time this algorithm had been implemented. It is also the fastest algorithm that currently exists for large multi-scalar multiplications.
A new algorithm for ecc multi-scalar multiplication
Traditional ecc multiplication algorithms represent elliptic curve points in 3-dimensions with `X, Y, Z` coordinates. This is in contrast to ‘affine’ coordinates, which just use an `X` and `Y` coordinate.
ECC operations can be split up into 3 distinct types: field additions, field multiplications and field inversions.
The problem with affine coordinates, is that elliptic curve addition requires 3 field multiplications and a field inversion. Inversions are about 250x more expensive than multiplications.
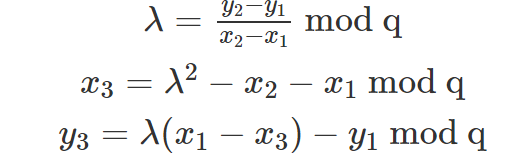
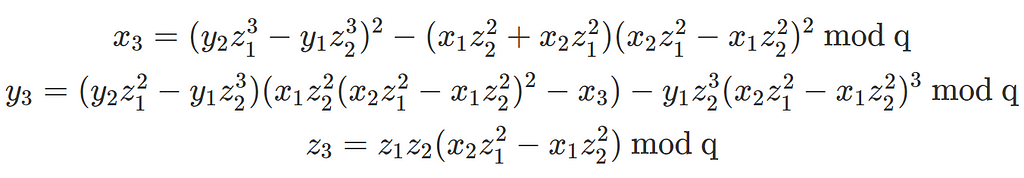
By adding a Z-coordinate, the field inversion is removed at the expense of adding 8 field multiplications.
Traditional ecc multiplication algorithms use the 3-coordinate representation because of this.
However, we exclusively work in affine coordinates. Our algorithms are constructed so that, when we need to perform point additions, we must perform many linearly independent additions. For each set of point additions, we use Montgomery’s batch inversion trick to compute all the required field inversions with a single field inversion, amortising away its high cost.
The result is an algorithm that is 30% faster than those that do not this technique.
Putting it all together
The result of this is that, on modern laptops, our privacy proof can be computed in a web browser in only 10 seconds. Advanced private transactions have finally become practical in a web-browser. Our latest in-development tech will continue to drop this number.
Looking into the future
Private transactions are just the tip of the iceberg. The most important goal for us over the next year is to support full programmability. Only by giving developers the tools to develop their own custom protocols and transaction flows will our vision of programmable private digital currencies be realised.
Our final architecture will support fully programmable privacy-preserving smart contracts, written in our new ZK-SNARK programming language Noir. Noir has been designed from the ground up to be optimized for compiling to our proving systems and for making privacy easy to work with.
The end goal is to support an active ecosystem of private cryptocurrencies, each with the ability to interface with existing L1 and L2 protocols, as well as DeFi protocols deployed directly onto Aztec’s rollup.
We have also not been idle with our R&D. Our latest cryptosystem, UltraPlonk, is close to deployment and will power our upgraded protocol architecture. UltraPlonk utilizes our latest plookup research, which enables efficient look-up tables within Plonk circuits. This is a major breakthrough that enables ZK-SNARK circuits to efficiently implement traditional algorithms that do not rely on prime-field arithmetic (e.g. AES128 encryption, SHA hashes, even basic things like integer arithmetic). It also allows us to efficiently add traditional memory abstractions into Noir, something completely foreign to existing proving systems.
We’re planning a full article that outlines our future plans and roadmap in detail. Stay tuned for more details!
![]()





